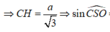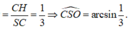Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,SD=avà SD vuông góc với mặt phẳng đáy. Tính góc giữa đường thẳng SA và mặt phẳng (SBD)
A. 45 ∘
B. a r c sin 1 4
C. 30 ∘
D. 60 ∘
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
17 tháng 7 2019
Đúng(0)
Những câu hỏi liên quan
CM
5 tháng 6 2018
Chọn C.
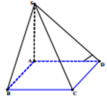
Vì SA ⊥ (ABCD) nên góc giữa đường thẳng SD và mặt phẳng (ABCD) là góc S D A ^
Tam giác SAD vuông tại A nên 
CM
7 tháng 12 2019
Đáp án là A
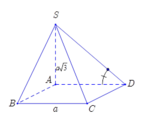
Ta có: S D ; A B C D ^ = S D ; A D ^ = S D A ^ .
Trong tam giác SAD có:
tan S D A ^ = S A A D = a 3 a = 3 ⇒ S D A ^ = 60 0 .
CM
11 tháng 1 2018
Đáp án C
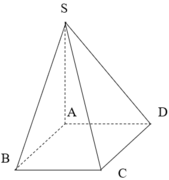
Ta thấy AD là hình chiếu vuông góc của SD lên (ABCD)
10 tháng 5 2023
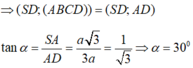
a: DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
b: (SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=căn 3
=>góc SDA=60 độ
CM
16 tháng 11 2017
Đáp án A.
Gọi H là hình chiếu của C trên SO và góc S O C ^ tù nên H nằm ngoài đoạn SO => CH ⊥ (SBD)
=> Góc tạo bởi SC và (SBD) là C S O ^
Lại có 
