Trong mặt phẳng tọa độ Oxy, gọi (H) là phần mặt phẳng chứa các điểm biểu diễn các số phức z thỏa mãn z 16 và z 16 có phần thực và phần ảo đều thuộc đoạn [ 0 ; 1 ] . Tính diện tích S của (H)
A. S = 256
B. S = 64 π
C. S = 16 4 − π
D. S = 32 6 − π
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tập hợp các điểm thuộc đường thẳng x = -2
b) Tập hợp các điểm thuộc đường thẳng y = 3
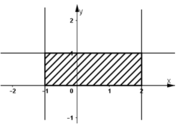
c) Tập hợp các điểm thuộc mặt phẳng nằm giữa hai đường thẳng song song x = -1 và x = 2 (hình có gạch sọc)
d) Phần mặt phẳng giới hạn bởi các đường thẳng song song y = 1 và y = 3( kể cả các điểm thuộc hai đường thẳng đó).
e) Các điểm thuộc hình chữ nhật với các cạnh nằm trên các đường thằng x = -2, x = 2 , y = -2, y = 2.

Phần thực của z thuộc đoạn [-1; 2]
⇔ -1 ≤ x ≤ 2.
phần ảo của z thuộc đoạn [0; 1]
⇔ 0 ≤ y ≤ 1.
Vậy tập hợp các điểm biểu diễn số phức z là hình gạch sọc dưới đây:

Đường phân giác của góc phần tư thứ hai và góc phần tư thứ tư.

Đường phân giác của góc phần tư thứ nhất và góc pần tư thứ ba.
Đáp án D.
Gọi z = x + y i x , y ∈ ℝ ⇒ M x ; y biểu diễn số phức z
Do z 16 có phần thực là và phần ảo thuộc đoạn 0 ; 1 nên
0 ≤ x 16 ≤ 1 0 ≤ y 16 ≤ 1 ⇒ 0 ≤ x , y ≤ 16
Mặt khác 16 z ¯ = 16 z z 2 = 16 x + y i x 2 + y 2 có phần thực là và phần ảo thuộc đoạn 0 ; 1 nên
x , y ≤ 0 16 x x 2 + y 2 ≤ 1 16 y x 2 + y 2 ≤ 1 ⇔ x 2 + y 2 − 16 x ≥ 0 x 2 + y 2 − 16 y ≥ 0
Minh họa hình vẽ, ta có phương trình đường thẳng OA là y = x , phương trình
x 2 + y 2 − 16 x = 0 ⇒ y = 16 x − x 2 y ≥ 0
Diện tích cần tìm là miền nằm ngoài 2 đường tròn x 2 + y 2 − 16 x = 0 và x 2 + y 2 − 16 y = 0 và nằm trong hình vuông MNPQ.
Diện tích hình quạt I O A ⏜ là S q u a t = 1 4 π 8 2 = 16 π ; S Δ I O A = 32
Diện tích phần giới hạn bởi cung OA và dây OA là S = 16 π − 32
Suy ra diện tích miền giao nhau của 2 đường tròn là: S G = 2 S = 32 π − 2 .
Diện tích cần tìm là:
S c t = 16 2 − π 8 2 + 32 π − 2 = 192 − 32 π = 32 6 − π