Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
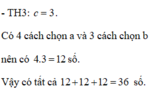
Đáp án B
Phương pháp: Xét từng trường hợp a = 3; b = 3; c = 3 rồi cộng các kết quả ta được số các số cần tìm.
Cách giải: Gọi số có ba chữ số là a b c ¯ .
- TH1: a = 3.
Có 4 cách chọn b và 3 cách chọn c nên có 4.3 = 12 số.
- TH2: b = 3
Có 4 cách chọn a và 3 cách chọn c nên có 4.3 = 12 số.
- TH3: c = 3.
Có 4 cách chọn a và 3 cách chọn b nên có 4.3 = 12 số.
Vậy có tất cả 12 + 12 + 12 = 36 số.
Chọn 2 chữ số còn lại từ {1;2;4;5} có: \(C_4^2=6\) cách
Hoán vị 3 chữ số: \(3!=6\) cách
Tổng cộng có: \(6.6=36\) số
1.
Chữ số hàng đơn vị có 4 cách chọn (từ 1,3,5,7)
Chọn và hoán vị 4 chữ số từ 6 chữ số còn lại: \(A_6^4\) cách
Tổng cộng: \(4.A_6^4\) cách
2.
Gọi chữ số cần lập có dạng \(\overline{abcd}\)
a.
Lập số có 4 chữ số bất kì (các chữ số đôi một khác nhau): \(A_6^4\) cách
Lập số có 4 chữ số sao cho số 0 đứng đầu: \(A_5^3\) cách
\(\Rightarrow A_6^4-A_5^3=300\) số
b.
Để số được lập là số chẵn \(\Rightarrow\) d chẵn
TH1: \(d=0\Rightarrow abc\) có \(A_5^3\) cách chọn
TH2: \(d\ne0\Rightarrow d\) có 2 cách chọn (từ 2;4)
a có 4 cách chọn (khác 0 và d), b có 4 cách chọn, c có 3 cách chọn
\(\Rightarrow2.4.4.3=96\) số
Tổng cộng: \(A_5^3+96=156\) số
Xác suất \(P=\dfrac{156}{300}=...\)
Câu 1:
Gọi số tổng quát là \(X=\overline{ab}\)
a có 9 cách chọn
b có9 cách chọn
=>Có 9*9=81(số)
Số cách chọn ngẫu nhiên 3 số từ tập A là \(C^3_{81}\left(cách\right)\)
Câu 2:
\(\overline{abc}\)
a có 9 cách
b có 9 cách
c có 8 cách
=>có 9*9*8=81*8=648(số)
Số cách chọn ngẫu nhiên 2 số từ tập A là \(C^2_{648}\left(cách\right)\)
\(\overline{abc}\)
c có 3 cách
a có 4 cách
b có 3 cách
=>Có 3*4*3=36 cách
a: Gọi số tự nhiên lập được là \(\overline{abc}\)
a có 5 cách chọn
b có 5 cách chọn
c có 5 cách chọn
Do đó: Có \(5\cdot5\cdot5=125\left(số\right)\) có 3 chữ số lập được từ các chữ số của tập hợp A
b: Gọi số tự nhiên cần tìm có dạng là \(\overline{abc}\)
a có 5 cách chọn
b có 4 cách chọn
c có 3 cách chọn
Do đó: Có 5*4*3=60 số có 3 chữ số khác nhau lập được từ tập hợp A
Gọi số cần tìm là \(\overline{abcdef}\)
TH1: 0,1,2 là 3 số cuối
=>\(\overline{abc012};\overline{abc210}\)
a có 6 cách
b có 5 cách
c có 4 cách
=>CÓ 6*5*4*2=240 cách
TH2: \(\overline{ab\left\{0,1,2\right\}f}\)
0,1,2 có 3!=6 cách
a có 5 cách
b có 4 cách
f có 3 cách
=>Có 360 cách
TH3: \(\overline{a\left\{0,1,2\right\}ef}\)
0,1,2 có 3!=6 cách
f có 2 cách
e có 5 cách
a có 4 cách
=>Có 6*3*5*4=360 cách
TH4: \(\overline{\left\{0,1,2\right\}def}\)
{0;1;2} có 4 cách
f có 3 cách
d có 5 cách
e có 4 cách
=>Có 4*3*5*4=240 cách
=>Có 120+120+360+360+240=1200 cách
TH1 (012)def : chọn a từ (1,2) có 2 cách
chọn b từ (012)/(a) có 2 cách
chọn c từ (012)/(ab) có 1 cách
chọn f chẵn từ (4,6) có 2 cách
với d và e chọn 2 số từ 4 số còn lại và xếp nên có 4A2 cách
vậy có 2.2.1.4A2.2 số
TH2 a(012)ef
xếp chỗ cho 3 số (012) có 3! cách
chọn f từ (4,6) có 2 cách
chọn ae từ 4 số còn lại và xếp có 4A2 cách
vậy có 3!.2.4A2 số
TH3 ab(012)f
tương tự TH2
TH4 : abc(012):
chọn f chẵn từ (0,2) có 2 cách
chọn e từ (012)/(a) có 2 cách
chọn d từ (012)/(ab) có 1 cách
với abc chọn 3 số từ 5 số còn lại và xếp nên có 5A3 cách
vậy có 2.2.1.5A3 số
tổng 4 TH ta có
2.2.1.4A2.2+3!.2.4A2+3!.2.4A2+2.2.1.5A3=624 số
