Gọi S là tập hợp những số có dạng x y z ¯ với x , y , z ∈ 1 ; 2 ; 3 ; 4 ; 5 . Số phần tử của tập hợp S là:
A. 5!
B. A 5 3
C. C 5 3
D. 5 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 9 2021
a)-Từ cthh X2O3 ,ta có: X hóa trị a, O hóa trị nên theo quy tắc hóa trị : 2a=3.II=>a=III
=>X hóa trị III.
-Từ cthh YH4 ,ta có : Y hóa trị b, H hóa trị I nên theo quy tắc hóa trị: 1b=4.I=>b=IV => Y hóa trị IV.
vì Z là hc gồm 2 ntố X và Y nên gọi cthh của Z là XyYx.
Áp dg quy tắc hóa trị vào cthh của Z, ta có: X hóa trị III, Y hóa trị IV
=>III.x=IV.y=> x/y=4/3
=> cthh dạng chung của Z là X4Y3.
CM
6 tháng 9 2019
Đáp án A
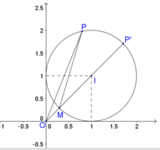
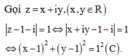
Gọi I là tâm của đường tròn (C).
Với mọi điểm P bất kì chạy trên S, ta có 
do đó số phức tương ứng với P có môđun lớn nhất khi và chỉ khi OP lớn nhất
O, M, P thẳng hàng và M nằm giữa O và P 
Phương trình đường thẳng OI: y = x. Tọa độ P’ là nghiệm của hệ phương trình :
Vậy số phức tương ứng với P có môđun lớn nhất bằng 1 + 2
23 tháng 11 2016
Ta có: x,y,z \(\in\)Z ,nên
\(A=\frac{x}{x+y}+\frac{y}{y+z}+\frac{z}{z+x}>\frac{x}{x+y+z}+\frac{y}{x+y+z}+\frac{z}{x+y+z}=\frac{x+y+z}{x+y+z}=1\)
\(\Rightarrow A>1\)
\(B=\frac{x}{x+y}+\frac{y}{y+z}+\frac{z}{z+x}>\frac{y}{x+y+z}+\frac{z}{x+y+z}+\frac{x}{x+y+z}=1\)
\(\Rightarrow B>1\)
Ta có: \(A+B=\left(\frac{x}{x+y}+\frac{y}{x+y}\right)+\left(\frac{y}{y+z}+\frac{z}{y+z}\right)+\left(\frac{z}{z+x}+\frac{x}{z+x}\right)=3\) và B > 1
Do đó A < 2.Vậy 1 < A < 2
=> A có giá trị là 1 số không thuộc tập hợp số nguyên
Phương pháp:
Sử dụng quy tắc nhân.
Cách giải:
Mỗi chữ số x, y, z đều có 5 cách chọn suy ra số phần tử của tập hợp S là: 5 3
Chọn: D