Tính tích phân I = ∫ 1 5 d x x 3 x + 1 ta được kết quả I = a ln 3 + b ln 5. Giá trị S = a 2 + a b + 3 b 2 là
A. 0
B. 4
C. 1
D. 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\int\dfrac{2dx}{x^2-5x}=\int\left(\dfrac{-2}{5x}+\dfrac{2}{5\left(x-5\right)}\right)dx=-\dfrac{2}{5}ln\left|x\right|+\dfrac{2}{5}ln\left|x-5\right|+C\)
\(\Rightarrow A=-\dfrac{2}{5};B=\dfrac{2}{5}\Rightarrow2A-3B=-2\)
b) \(\int\dfrac{x^3-1}{x+1}dx=\int\dfrac{x^3+1-2}{x+1}dx=\int\left(x^2-x+1-\dfrac{2}{x+1}\right)dx=\dfrac{1}{3}x^3-\dfrac{1}{2}x^2+x-2ln\left|x+1\right|+C\)
\(\Rightarrow A=\dfrac{1}{3};B=\dfrac{1}{2};E=-2\Rightarrow A-B+E=-\dfrac{13}{6}\)

+) A nhỏ nhất khi |5-x| nhỏ nhất. vì |5-x| là một số luôn lớn hơn hoặc bằng 0 nhỏ nhất là = 0
Vậy A nhỏ nhất = 2/3 khi và chỉ khi 5-x = 0 => x = 5
+)B nhỏ nhất khi (x-2)^2 là nhỏ nhất. (x-2)^2 luôn lớn hơn hoặc bằng 0 nhỏ nhất là bằng 0
Vậy B nhỏ nhất = 1 khi và chỉ khi x-2 = 0 => x = 2
+) C lớn nhất khi |x - 4| nhỏ nhất.
|x - 4| nhỏ nhất = 0
Vậy C lớn nhất = 0,5 - 0 = 0,5 khi và chỉ khi x- 4 = 0 => x = 4

\(a,y'=8x^3-9x^2+10x\\ \Rightarrow y''=24x^2-18x+10\\ b,y'=\dfrac{2}{\left(3-x\right)^2}\\ \Rightarrow y''=\dfrac{4}{\left(3-x\right)^3}\)
\(c,y'=2cos2xcosx-sin2xsinx\\ \Rightarrow y''=-5sin\left(2x\right)cos\left(x\right)-4cos\left(2x\right)sin\left(x\right)\\ d,y'=-2e^{-2x+3}\\ \Rightarrow y''=4e^{-2x+3}\)

đặt t = lnx
tôi ko biết \(\varepsilon\) trong bài là gì, tuy nhiên nếu nó là số bất kì thì xét 2 TH sau để biết đk t
TH1: \(\varepsilon\in\left(0;1\right)\)
TH2: \(\varepsilon>1\)

\(I=\int_1^4\frac{\ln\left(5-x\right)+x^3}{x^2}dx=\int\limits_1^4\frac{\ln\left(5-x\right)}{x^2}dx+\int\limits^4_1xdx=I_1+I_2\)
\(I_1=\int_1^4\frac{\ln\left(5-x\right)}{x^2}dx:\)\(\begin{cases}u=\ln\left(5-x\right)\\v'=\frac{1}{x^2}\end{cases}\)\(\Rightarrow\begin{cases}u'=-\frac{1}{5-x}\\v=-\frac{1}{x}\end{cases}\)
\(I_1=-\frac{1}{x}\ln\left(5-x\right)|^4_1-\int\limits^4_1\frac{1}{x\left(5-x\right)}dx\)\(=2\ln2+\frac{1}{5}\int\limits^4_1\left(\frac{1}{x-5}-\frac{1}{x}\right)dx\)
\(=2\ln2-\frac{4}{5}\ln2=\frac{6}{5}\ln2\)
\(I_2=\int\limits^4_1xdx=\frac{x^2}{2}|^4_1=\frac{15}{2}\)
\(I=\frac{15}{2}+\frac{6}{5}\ln2\)

a) Bất phương trình đã cho tương đương với hệ sau:
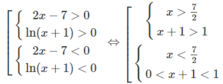
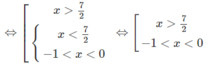
Vậy tập nghiệm là (−1;0) ∪ (7/2; + ∞ )
b) Tương tự câu a), tập nghiệm là (1/10; 5)
c) Đặt t = log 2 x , ta có bất phương trình 2 t 3 + 5 t 2 + t – 2 ≥ 0 hay (t + 2)(2 t 2 + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ 1/2
Suy ra 1/4 ≤ x ≤ 1/2 hoặc x ≥ 2
Vậy tập nghiệm của bất phương trình đã cho là: [1/4; 1/2] ∪ [ 2 ; + ∞ )
d) Bất phương trình đã cho tương đương với hệ:
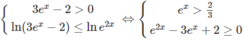
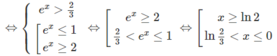
Vậy tập nghiệm là (ln(2/3); 0] ∪ [ln2; + ∞ )
Đáp án D