Tập xác định của hàm số y = cot x là
A. D = ℝ \ k π 2 k ∈ ℤ
B. D = ℝ \ k π k ∈ ℤ
C. D = ℝ \ k 2 π k ∈ ℤ
D. D = ℝ \ π 2 + k π k ∈ ℤ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Hàm số y = sin 2x thỏa mãn tính chất trên, các hàm số y = tan x, y = cot x cần điều kiện của x.

Đáp án B
TXĐ của hàm y = tanx là D = ℝ \ π 2 + k π | k ∈ ℤ nên TXĐ của hàm y = tan 2 x là D = ℝ \ π 4 + k π 2 | k ∈ ℤ
TXĐ của hàm y = cot x là D = ℝ \ k π | k ∈ ℤ nên TXĐ của hàm y = cot 2 x là D = ℝ \ k π 2 | k ∈ ℤ

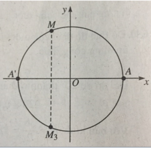
-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.
Vậy (-5π)/2 < -6,32 < -2π.
Do đó điểm M nằm ở góc phần tư thứ II.
Đáp án: B

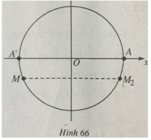
(h.66) Ta có
A M 2 = MA’ = MA + AA’
Suy ra
Sđ A M 2 = -α + π + k2π, k ∈ Z.
Vậy đáp án là B.
6.13. (h.67) Ta có
Sđ A M 3 = -sđ AM = -α + k2π, k ∈ Z.
Đáp án: D

Đáp án D
(2) sai vì xảy ra trường hợp x 0 không thuộc K . Ví dụ hàm
![]()

Chọn D
Hàm số y= cot(2x-π/3)+2 xác định khi và chỉ khi sin(2x-π/3)≠0
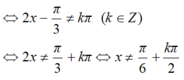

Đáp án D
(1) Nếu f ' x 0 = 0 hoặc f ' x 0 không xác định trên K thì x 0 có thể là điểm cực trị của hàm số trên K. Còn nếu f ' x 0 ≠ 0 thì x 0 không thể nào là điểm cực trị của hàm số trên K. Vậy phát biểu (1) đúng.
(2) Nếu x 0 ∉ K mà qua điểm x 0 , f ' x có sự đổi dấu thì x 0 không phải là điểm cực trị của hàm số f. Vậy phát biểu (2) sai.
Đáp án B
Hàm số đã cho xác đinh khi s inx ≠ 0 ⇔ x ≠ k π k ∈ ℤ