Cho hàm số f(x) xác định trên R thỏa mãn f ' x = 4 x + 3 v à f 1 = − 1 . Biết rằng phương trình f x = 10 có hai nghiệm thực x 1 , x 2 . Tính tổng log 2 x 1 + log 2 x 2
A. 8
B. 16
C. 4
D. 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
21 tháng 9 2018
Đúng(0)
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
16 tháng 4 2021
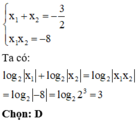
Lời giải:
Thay $x=0$ vào điều kiện đề thì $f(1)=0$ hoặc $f(1)=-1$
Đạo hàm 2 vế:
$4f(2x+1)f'(2x+1)_{2x+1}=1+3f(1-x)^2f'(1-x)_{1-x}$
Thay $x=0$ vô thì:
$4f(1)f'(1)=1+3f(1)^2f'(1)$
Nếu $f(1)=0$ thì hiển nhiên vô lý
Nếu $f(1)=-1$ thì: $-4f'(1)=1+3f'(1)\Rightarrow f'(1)=\frac{-1}{7}$
PTTT tại $x=1$ có dạng:
$y=f'(1)(x-1)+f(1)=\frac{-1}{7}(x-1)-1=\frac{-x}{7}-\frac{6}{7}$
