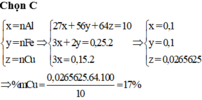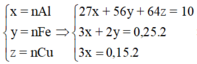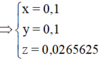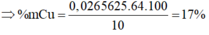10 g hỗn hợp Cu và Al khi tác dụng với dung dịch HNO3 rất đặc sinh ra 4,48l CO2 (đktc). Thành phần % của Cu trong hỗn hợp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 1 2017
Gọi nAl = x (mol), nCu = y (mol); nNO2 =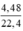 
= 0,2 mol
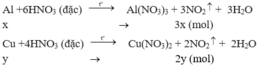
Theo pt: nNO2(1) = 3. nAl = 3.x mol
nNO2(2) = 2. nCu = 2y mol
⇒ Tổng nNO2 = 3x + 2y = 0,2 mol
Ta có hệ phương trình
H
27 tháng 8 2021
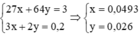
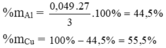
Gọi $n_{Cu} = a(mol) ; n_{Al} = b(mol) \Rightarrow 64a + 27b = 3(1)$
$Cu^0 \to Cu^{+2} + 2e$
$Al^0 \to Al^{+3} + 3e$
$N^{+5} + 1e \to N^{+4}$
Bảo toàn electron :
$2a + 3b = 0,2(2)$
Từ (1)(2) suy ra $a = \dfrac{3}{115} ; b = \dfrac{17}{345}$
\(\%m_{Cu}=\dfrac{\dfrac{3}{115}.64}{3}.100\%=55,65\%\\ \%m_{Al}=100\%-55,65\%=44,35\%\)
27 tháng 8 2021
Gọi số mol của Cu và Al lần lượt là x,y (mol) (x,y>0)
\(Cu+4HNO_{3\left(đ\right)}\underrightarrow{to}Cu\left(NO_3\right)_2+2NO_2+2H_2O\\ x..................................2x\left(mol\right)\\ Al+6HNO_{3\left(đ\right)}\underrightarrow{to}Al\left(NO_3\right)_3+3NO_2+3H_2O\\ y...............................3y\left(mol\right)\)
\(\left\{{}\begin{matrix}64x+27y=3\\2x+3y=0,2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{115}\\y=\dfrac{17}{345}\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\%m_{Cu}=\dfrac{\dfrac{3}{115}.64}{3}.100\approx55,652\%\\\%m_{Al}\approx44,348\%\end{matrix}\right.\\ \)
H
28 tháng 10 2021
Al không tác dụng với $HNO_3$ đặc nguội
$Cu + 4HNO_3 \to Cu(NO_3)_2 + 2NO_2 + 2H_2O$
$n_{Cu} = \dfrac{1}{2}n_{NO_2} = \dfrac{1}{2}.\dfrac{3,36}{22,4} = 0,075(mol)$
Mặt khác : $n_{NO} = \dfrac{7,84}{22,4} = 0,35(mol)$
Bảo toàn electron : $2n_{Cu} + 3n_{Al} = 3n_{NO}$
$\Rightarrow n_{Al} = \dfrac{0,35.3 - 0,075.2}{3} = 0,3(mol)$
$m = 0,075.64 + 0,3.27 = 12,9(gam)$
21 tháng 12 2019
2.
Ta có Fe và Al thụ động với HNO3đặc nguội nên chỉ có Cu Phản ứng
Phần 1 : BTe\(\rightarrow\) nCu = 0,1 mol
Phần 2:
Đặt nAl = a ; nFe = b
BTKL\(\rightarrow\)27a + 56b = 11
BTe \(\rightarrow\) 3a + 2b = 0,8
\(\rightarrow\)a= 0,2 ; b = 0,1
\(\rightarrow\)mAl = 10,8 ; mFe = 11,2 gam