Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có nghiệm thuộc đoạn 0 ; 1 ; x 3 + x 2 + x = m x 2 + 1 2
A. m ≥ 1
B. m ≤ 1
C. 0 ≤ m ≤ 1
D. 0 ≤ m ≤ 3 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
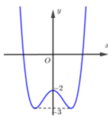
Dựa vào đồ thị hàm số y = x 4 − 2 x 2 − 2
Suy ra − 3 < m < − 2 là giá trị cần tì

x^3-x^2(m+3)+x(3m+2)-2m=0
=>(x-1)(x^2-(m+2)x+2m)=0
=>x=1 hoặc x^2-(m+2)x+2m=0
Để PT có 3 nghiệm thì (m+2)^2-4*2m>0 và 1^2-(m+2)+2m<>0
=>m<>1 và m<>2
=>x2=(m+2-m+2)/2=2 và x3=(m+2+m-2)/2=m
Để tạo thành cấp sô nhân thì
x1<x2<m hoặc m<x1<x2 hoặc x1<m<x2
=>m*1=2^2 hoặc 2m=1 hoặc m^2=2
=>m=4 hoặc m=1/2 hoặc m=căn 2

Đáp án C
Ta có f x = 2 x + m − 1 x + 1 → f ' x = 3 − m x + 1 2 ; ∀ x ∈ 1 ; 2
TH1: Với m < 3 , suy ra f ' x > 0 ; ∀ ∈ 1 ; 2 ⇒ f 2 = 1 ⇔ 3 + m 3 = 1 ⇔ m = 0 (nhận)
TH2: Với m>3 suy ra f ' x < 0 ; ∀ ∈ 1 ; 2 ⇒ f 1 = 1 ⇔ 1 + m 2 = 1 ⇔ m = 1 (loại)
Vậy m = 0 là giá trị cần tìm
Đáp án D
Ta có P T ⇔ x 3 + x x 2 + 1 2 + x 2 x 2 + 1 2 = x x 2 + 1 + x x 2 + 1 2
Đặt t = x x 2 + 1 ⇒ t ' = 1 − x 2 x 2 + 1 ≥ 0 ∀ x ∈ 0 ; 1 ⇒ t ∈ 0 ; 1 2
Xét f t = t 2 + t t ∈ 0 ; 1 2
Ta có f ' t = 2 t + 1 > 0 t ∈ 0 ; 1 2
min 0 ; 1 2 f t = f 0 = 0 ; max 0 ; 1 2 f t = f 1 2 = 3 4 .
Do đó để phương trình đã cho có nghiệm thì 0 ≤ m ≤ 3 4