Cho hai số thực m, n thỏa mãn n<m. Khẳng định nào sau đây đúng?
A. 3 − 2 − m 2 > 9 3 + 11 2 n 6 .
B. 3 − 2 − m 2 ≤ 9 3 + 11 2 n 6 .
C. 3 − 2 − m 2 < 9 3 + 11 2 n 6 .
D. 3 − 2 − m 2 = 9 3 + 11 2 n 6 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P\ge\sqrt{3-m^2+3-n^2}=\sqrt{2}\)
\(P_{min}=\sqrt{2}\) khi \(\left[{}\begin{matrix}\sqrt{3-m^2}=0\\\sqrt{3-n^2}=0\end{matrix}\right.\) \(\Leftrightarrow\left(m;n\right)=\left(1;\sqrt{3}\right);\left(\sqrt{3};1\right)\)
\(P\le\sqrt{2\left(3-m^2+3-n^2\right)}=2\)
\(P_{max}=2\) khi \(m=n=\sqrt{2}\)

Chọn D.
Phương trình ![]()
Ta thấy 1 - (m + 3) + m + 2 = 0 nên 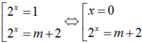
Từ đó 2x = m + 2 cần phải có nghiệm thực khác 0 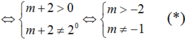
Khi đó 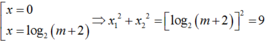
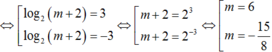 thỏa mãn (*)
thỏa mãn (*)
Kết hợp với m > 0 đề bài cho thì ta được m = 6 thỏa mãn.

Ta có
log 4 n - 3 + log 4 n + 9 = 3 ⇔ log 4 n - 3 n + 9 = 3 ⇔ n 2 + 6 b - 91 = 0 ⇔ n = n = - 13 z = 1 + i 7 = 1 + i 1 + i 2 3 = 8 - 8 i
Vậy tổng phần thực và phần ảo của số phức z bằng 0
Đáp án D

M a b a b 9 11 7 là như thế nào vậy bạn? Bạn cần viết rõ để mọi người hiểu đề của bạn hơn.
Đáp án A
3 − 2 − m 2 > 9 3 + 11 2 n 6 ⇔ 3 − 2 − m 2 3 − 2 n 2 > 3 + 2 n 2 3 − 2 n 2
⇔ 3 − 2 n − m 2 > 1 do 0 < 3 − 2 < 1 ⇒ n − m 2 < 0 ⇔ m > n