Gọi S là tập nghiệm của phương trình 2 2 x - 1 - 5 . 2 x - 1 + 3 = 0 . Tìm S.
A. S = 1 ; log 2 3
B. S = 0 ; log 2 3
C. S = 1 ; log 3 2
D. S = {1}
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 1 2018
Đáp án A
Phương pháp:
Đặt ẩn phụ, đưa về phương trình bậc hai một ẩn. Giải phương trình và suy ra ẩn t.
Cách giải:
Phương trình đã cho trở thành
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
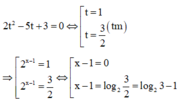
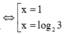
Ta có tập nghiệm của phương trình là:
\(\left(x+2\right)\left(2x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\2x-1=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\2x=1\\x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{1}{2}\\x=3\end{matrix}\right.\)
Tập hợp S là:
\(S=\left\{-2;\dfrac{1}{2};3\right\}\)
Lần lược các phương án:
A. \(-2\in S\) (đúng)
B. \(3\in S\) (đúng)
C. \(2\in S\) (Sai)
D. \(\dfrac{1}{2}\in S\) (Đúng)
⇒ Chọn C
. D. 
.
là nghiệm của phương trình:
. B.
. C.
. D.
.
có tập nghiệm S là :
. B. S = {- 4}. C. S = {4;-4}. D. S = {4}. 
ABC có AD là đường phân giác (D
BC), biết 
và CD = 15cm. Độ dài đoạn BD là:
theo tỉ số k thì 
. D. – k2.
CM
11 tháng 4 2017
a. Đúng
Vì x 2 + 1 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
4x – 8 + (4 – 2x) = 0 ⇔ 2x – 4 = 0 ⇔ 2x = 4 ⇔ x = 2
b. Đúng
Vì x 2 – x + 1 = x - 1 / 2 2 + 3/4 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
(x + 2)(2x – 1) – x – 2 = 0 ⇔ (x + 2)(2x – 2) = 0
⇔ x + 2 = 0 hoặc 2x – 2 = 0 ⇔ x = - 2 hoặc x = 1
c. Sai
Vì điều kiện xác định của phương trình là x + 1 ≠ 0 ⇔ x ≠ - 1
Do vậy phương trình 
không thể có nghiệm x = - 1
d. Sai
Vì điều kiện xác định của phương trình là x ≠ 0
Do vậy x = 0 không phải là nghiệm của phương trình 
CM
7 tháng 2 2019
Chọn C
Điều kiện
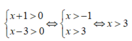
Ta có: log5(x+1) + log5( x-3) = 1
Tương đương : log5[(x+1)( x-3)] = 1 hay ( x+1) (x-3) = 5
=> x2- 3x+ x- 3= 5 nên x2- 2x-8= 0
Do đó; x= -2 hoặc x= 4
Mà x= -2 loại do đó đáp án đúng là C .
AH
Akai Haruma
Giáo viên
16 tháng 5 2021
Lời giải:
Đặt $\sqrt{x+2}=t(t\geq 0)$ thì pt trở thành:
$t^2-2-2t-m-3=0$
$\Leftrightarrow t^2-2t-(m+5)=0(*)$
Để PT ban đầu có 2 nghiệm pb thì PT $(*)$ có 2 nghiệm không âm phân biệt.
Điều này xảy ra khi \(\left\{\begin{matrix} \Delta'=1+m+5>0\\ S=2>0\\ P=-(m+5)\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m>-6\\ m\leq -5\end{matrix}\right.\)
Đáp án B.
Đáp án A