Cho hàm số y = x 3 + 3 x 2 − 9 x + 5 có đồ thị (C) . Gọi A, B là giao điểm của (C) và trục hoành. Số điểm M ∈ C không trùng với A và B sao cho A M B ⏜ = 90 ° là:
A.2
B.0
C.3
D.1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 4 2018
Trước hết xin nói ngay rằng đồ thị của hàm số y = (2x - 1)(x - 1) là một parabol, không có đường tiệm cận nào cả.
Có lẽ bạn muốn nói đến hàm số y = (2x - 1)/(x - 1).
Nếu đúng vậy thì đồ thị của hàm số là một hyperbol vuông góc có hai đường tiệm cận là đường thẳng x = 1 và đường thẳng y = 2.
Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)
10 tháng 4 2018
Trước hết xin nói ngay rằng đồ thị của hàm số y = (2x - 1)(x - 1) là một parabol, không có đường tiệm cận nào cả.
Có lẽ bạn muốn nói đến hàm số y = (2x - 1)/(x - 1).
Nếu đúng vậy thì đồ thị của hàm số là một hyperbol vuông góc có hai đường tiệm cận là đường thẳng x = 1 và đường thẳng y = 2.
Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)
D
19 tháng 4 2020
2, Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)
20 tháng 12 2022
a: Để (d)//Ox thì m-1=0
=>m=1
b: Thay x=-1 và y=1 vào (d), ta được:
-m+1+m=1
=>1=1(luôn đúng)
c: Thay x=\(\dfrac{2-\sqrt{3}}{2}\) và y=0 vào (d), ta đc:
\(\left(m-1\right)\cdot\dfrac{2-\sqrt{3}}{2}+m=0\)
=>\(\left(m-1\right)\cdot\left(2-\sqrt{3}\right)+2m=0\)
=>\(2m-\sqrt{3}m-2+\sqrt{3}+2m=0\)
=>\(m\left(4-\sqrt{3}\right)=2-\sqrt{3}\)
=>\(m=\dfrac{2-\sqrt{3}}{4-\sqrt{3}}\)
22 tháng 12 2021
a: Thay x=3 và y=0 vào (1), ta được:
\(6-3m=0\)
hay m=2
CM
27 tháng 9 2018
+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.
AH
Akai Haruma
Giáo viên
27 tháng 11 2023
Lời giải:
a. Vì đths đi qua $A(-2;3)$ nên:
$y_A=(2m+5)x_A-1$
$\Rightarrow 3=(2m+5)(-2)-1\Rightarrow m=\frac{-7}{2}$
b. ĐTHS sau khi tìm được $m$ có pt: $y=-2x-1$. Bạn có thể tự vẽ
c. ĐTHS cắt trục hoành tại điểm có hoành độ -3, tức là đi qua điểm $(-3,0)$
$\Rightarrow 0=(2m+5)(-3)-1$
$\Rightarrow m=\frac{-8}{3}$
16 tháng 11 2023
a: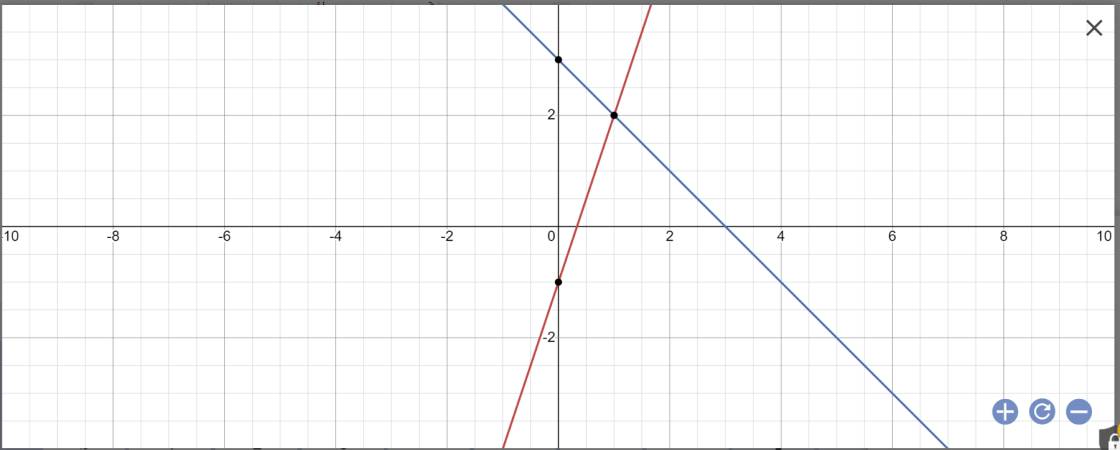 
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\3x-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=0\end{matrix}\right.\)
Vậy: A(1/3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-x=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=3\end{matrix}\right.\)
Vậy: B(3;0)
Tọa độ C là:
\(\left\{{}\begin{matrix}3x-1=-x+3\\y=3x-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x=4\\y=3x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-1=2\end{matrix}\right.\)
Vậy: C(1;2)
c: Gọi \(\alpha\) là góc tạo bởi (d1) với trục Ox
\(tan\alpha=a=3\)
=>\(\alpha\simeq71^033'\)
Đáp án A
Xét PT:
x 3 + 3 x 2 − 9 x + 5 = 0 ⇔ x + 5 x − 1 2 = 0 ⇔ x = 1 x = − 5 ⇒ A 1 ; 0 , B − 5 ; 0
M x ; y ∈ C ⇒ A M → = x − 1 ; y , B M → = x + 5 ; y điều kiện góc A M B = 90 0
⇔ A M → . B M → = 0 ⇔ x − 1 x + 5 + y 2 = 0 ⇔ x − 1 x + 5 + x − 1 4 x + 5 2 = 0 ⇔ x − 1 x + 5 1 + x − 1 3 x + 5 = 0
⇔ 1 + x − 1 3 x + 5 = 0 ( do x ≠ 1, x ≠ − 5 )
Xét hàm số f ( x ) = 1 + x − 1 3 x + 5 có:
f ' x = 3 x − 1 2 x + 5 + x − 1 3 = x − 1 2 4 x + 14
Dễ thấy hàm số có một cực tiểu duy nhất x = − 7 2 với GTCT là y<0 . Do vậy PT f(x)=0 có hai nghiệm hay tồn tại hai điểm M thỏa mãn điều kiện.