Trong không gian Oxyz, cho điểm E(8;1;1). Viết phương trình mặt phẳng α qua E và cắt chiều dương các trục Ox, Oy, Oz lần lượt tại A, B, C sao cho OG nhỏ nhất với G là trọng tâm tam giác ABC.
A. x + 2 y + 2 z - 12 = 0
B. x + y + 2 z - 11 = 0
C. 2 x + y + z - 18 = 0
D. 8 x + y + z - 66 = 0




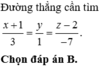


Sử dụng phương trình theo đoạn chắn của
mặt phẳng và áp dụng BĐT Bunhiacopski.
Chọn A.