Tính đạo hàm của hàm số y = log ( 2 3 e x ) . A. y ' = 3 e x ln 2 B. y ' = 1...

PT

Pham Trong Bach

2 tháng 2 2018

Tính đạo hàm của hàm số y = log ( 2 3 e x ) . A. y ' = 3 e x ln 2 B. y ' = 1 3 e x . ln 2 C. y ' = 1 3 e x D. y ' = 1 ln 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

2 tháng 2 2018

Đúng(0)

N

nanako

28 tháng 10 2021

Tính đạo hàm của hàm số sau:

a) $y=ln\left(1+\sqrt{3x-1}\right)$

b) $y=log\left(2sin^2x-1\right)$

c) $y=3^{x^3+3x+1}e^x$

#Toán lớp 12

1

NV

Nguyễn Việt Lâm

Giáo viên

1 tháng 11 2021

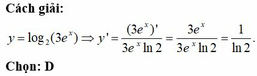
a.

$y'=\dfrac{\left(1+\sqrt{3x-1}\right)'}{1+\sqrt{3x-1}}=\dfrac{3}{2\left(1+\sqrt{3x-1}\right)\sqrt{3x-1}}$

b.

$y'=\dfrac{\left(2sin^2x-1\right)'}{\left(2sin^2x-1\right).ln10}=\dfrac{2sin2x}{\left(2sin^2x-1\right)ln10}$

c.

$y'=\left(3x^2+3\right)3^{x^3+3x+1}.e^x.ln3+3^{x^3+3x+1}.e^x$

Đúng(0)

B

Buddy

13 tháng 8 2023

Tính đạo hàm cấp hai của mỗi hàm số sau:

a) $y = 2{x^4} - 3{x^3} + 5{x^2}$

b) $y = \frac{2}{{3 - x}}$

c) $y = \sin 2x\cos x$

d) $y = {e^{ - 2x + 3}}$

e) $y = \ln (x + 1)$

f) $y = \ln ({e^x} + 1)$

#Toán lớp 11

3

HQ

Hà Quang Minh

Giáo viên

22 tháng 8 2023

$a,y'=8x^3-9x^2+10x\\ \Rightarrow y''=24x^2-18x+10\\ b,y'=\dfrac{2}{\left(3-x\right)^2}\\ \Rightarrow y''=\dfrac{4}{\left(3-x\right)^3}$

Đúng(1)

HQ

Hà Quang Minh

Giáo viên

22 tháng 8 2023

$c,y'=2cos2xcosx-sin2xsinx\\ \Rightarrow y''=-5sin\left(2x\right)cos\left(x\right)-4cos\left(2x\right)sin\left(x\right)\\ d,y'=-2e^{-2x+3}\\ \Rightarrow y''=4e^{-2x+3}$

Đúng(1)

PT

Phạm Trần Phát

18 tháng 11 2023

4. Tính đạo hàm của các hàm số sau:

a) $y = (3x^2-4x+1)^{-4}$

b) $y = 3^{x^2-1} + e^{-x+1}$

c) $y = \ln (x^2-4x) + \log_{3} (2x-1)$

d) $y =x . \ln x + 2^{\frac{x-1}{x+1}}$

e) $y = x^{-7} - \ln (x^2-1)$

#Toán lớp 12

2

2611

18 tháng 11 2023

`a)TXĐ:R\\{1;1/3}`

`y'=[-4(6x-4)]/[(3x^2-4x+1)^5]`

`b)TXĐ:R`

`y'=2x. 3^[x^2-1] ln 3-e^[-x+1]`

`c)TXĐ: (4;+oo)`

`y'=[2x-4]/[x^2-4x]+2/[(2x-1).ln 3]`

`d)TXĐ:(0;+oo)`

`y'=ln x+2/[(x+1)^2].2^[[x-1]/[x+1]].ln 2`

`e)TXĐ:(-oo;-1)uu(1;+oo)`

`y'=-7x^[-8]-[2x]/[x^2-1]`

Đúng(3)

AH

Akai Haruma

Giáo viên

18 tháng 11 2023

Lời giải:
a.

$y'=-4(3x^2-4x+1)^{-5}(3x^2-4x+1)'$

$=-4(3x^2-4x+1)^{-5}(6x-4)$

$=-8(3x-2)(3x^2-4x+1)^{-5}$

b.

$y'=(3^{x^2-1})'+(e^{-x+1})'$

$=(x^2-1)'3^{x^2-1}\ln 3 + (-x+1)'e^{-x+1}$

$=2x.3^{x^2-1}.\ln 3 -e^{-x+1}$

c.

$y'=\frac{(x^2-4x)'}{x^2-4x}+\frac{(2x-1)'}{(2x-1)\ln 3}$

$=\frac{2x-4}{x^2-4x}+\frac{2}{(2x-1)\ln 3}$

d.

$y'=(x\ln x)'+(2^{\frac{x-1}{x+1}})'=x(\ln x)'+x'\ln x+(\frac{x-1}{x+1})'.2^{\frac{x-1}{x+1}}\ln 2$

$=x.\frac{1}{x}+\ln x+\frac{2}{(x+1)^2}.2^{\frac{x-1}{x+1}}\ln 2\\ =1+\ln x+\frac{2^{\frac{2x}{x+1}}\ln 2}{(x+1)^2}$

e.

$y'=-7x^{-8}-\frac{(x^2-1)'}{x^2-1}=-7x^{-8}-\frac{2x}{x^2-1}$

Đúng(3)

B

Buddy

20 tháng 8 2023

Tính đạo hàm của các hàm số sau:

a) $y = \left( {{x^2} + 3x - 1} \right){e^x}$;

b) $y = {x^3}{\log _2}x$.

#Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

20 tháng 8 2023

a: $y'=\left(x^2+3x-1\right)'\cdot e^x+\left(x^2+3x-1\right)\cdot\left(e^x\right)'$

$=e^x\left(2x+3\right)+\left(x^2+3x-1\right)\cdot e^x$

$=e^x\left(x^2+5x+2\right)$

b: $y'=\left(x^3\right)'\cdot log_2x+x^3\cdot\left(log_2x\right)'$

$=3x^2\cdot log_2x+x^3\cdot\dfrac{1}{x\cdot ln2}$

Đúng(1)

B

Buddy

20 tháng 8 2023

Tính đạo hàm của các hàm số sau:

a) $y = x{\log _2}x$;

b) $y = {x^3}{e^x}$.

#Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

20 tháng 8 2023

a: $y'=\left(x\cdot log_2x\right)'=log_2x+x\cdot\dfrac{1}{x\cdot ln2}=log_2x+\dfrac{1}{ln2}$

b: $y'=\left(x^3e^x\right)'=\left(x^3\right)'\cdot e^x+x^3\cdot\left(e^x\right)'$

$=3x^2\cdot e^x+x^3\cdot e^x$

Đúng(0)

B

Buddy

20 tháng 8 2023

Tính đạo hàm của các hàm số sau:

a) $y = \left( {{x^2} - x} \right){.2^x}$;

b) $y = {x^2}{\log _3}x$;

c) $y = {e^{3x + 1}}$.

#Toán lớp 11

1

HQ

Hà Quang Minh

Giáo viên

22 tháng 9 2023

a) $y' = {\left( {{x^2} - x} \right)^\prime }{.2^x} + \left( {{x^2} - x} \right).{\left( {{2^x}} \right)^\prime } = \left( {2{\rm{x}} - 1} \right){.2^x} + \left( {{x^2} - x} \right){.2^x}.\ln 2$.

b) $y' = {\left( {{x^2}} \right)^\prime }.{\log _3}x + {x^2}.{\left( {{{\log }_3}x} \right)^\prime } = 2{\rm{x}}.{\log _3}x + {x^2}.\frac{1}{{x\ln 3}} = 2{\rm{x}}.{\log _3}x + \frac{x}{{\ln 3}}$.

c) Đặt $u = 3{\rm{x}} + 1$ thì $y = {e^u}$. Ta có: $u{'_x} = {\left( {3{\rm{x}} + 1} \right)^\prime } = 3$ và $y{'_u} = {\left( {{e^u}} \right)^\prime } = {e^u}$.

Suy ra $y{'_x} = y{'_u}.u{'_x} = {e^u}.3 = 3{{\rm{e}}^{3{\rm{x}} + 1}}$.

Vậy $y' = 3{{\rm{e}}^{3{\rm{x}} + 1}}$.

Đúng(0)

B

Buddy

13 tháng 8 2023

Tính đạo hàm của mỗi hàm số sau:

a) $y = \left( {{x^2} + 2x} \right)\left( {{x^3} - 3x} \right)$

b) $y = \frac{1}{{ - 2x + 5}}$

c) $y = \sqrt {4x + 5} $

d) $y = \sin x\cos x$

e) $y = x{e^x}$

f) $y = {\ln ^2}x$

#Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

14 tháng 8 2023

a: $y'=\left(x^2+2x\right)'\left(x^3-3x\right)+\left(x^2+2x\right)\left(x^3-3x\right)'$

$=\left(2x+2\right)\left(x^3-3x\right)+\left(x^2+2x\right)\left(3x^2-3\right)$

$=2x^4-6x^2+2x^3-6x+3x^4-3x^2+6x^3-6x$

$=5x^4+8x^3-9x^2-12x$

b: y=1/-2x+5

=>$y'=\dfrac{2}{\left(2x+5\right)^2}$

c: $y'=\dfrac{\left(4x+5\right)'}{2\sqrt{4x+5}}=\dfrac{4}{2\sqrt{4x+5}}=\dfrac{2}{\sqrt{4x+5}}$

d: $y'=\left(sinx\right)'\cdot cosx+\left(sinx\right)\cdot\left(cosx\right)'$

$=cos^2x-sin^2x=cos2x$

e: $y=x\cdot e^x$

=>$y'=e^x+x\cdot e^x$

f: $y=ln^2x$

=>$y'=\dfrac{\left(-1\right)}{x^2}=-\dfrac{1}{x^2}$

Đúng(1)

B

Buddy

17 tháng 8 2023

Tính đạo hàm của các hàm số sau:a) $y = {\left( {\frac{{2x - 1}}{{x + 2}}} \right)^5}$b) $y = \frac{{2x}}{{{x^2} + 1}}$;c) $y = {e^x}{\sin ^2}x$; d) \(y = \log (x + \sqrt x...

Đọc tiếp

#Toán lớp 11

1

BN

Bùi Nguyên Khải

17 tháng 8 2023

tham khảo:

a)$y'\left(x\right)=5\left(\dfrac{2x-1}{x+2}\right)^4.\dfrac{\left(x+2\right)\left(2\right)-\left(2x-1\right).1}{\left(x+2\right)^2}$

$=\dfrac{10\left(2x-1\right)\left(x+2\right)^3}{\left(x+2\right)^4}=\dfrac{20x-50}{\left(x+2\right)^4}$

b)$y'\left(x\right)=\dfrac{2\left(x^2+1\right)-2x\left(2x\right)}{\left(x^2+1\right)^2}$$=\dfrac{2\left(1-x^2\right)}{\left(x^2+1\right)^2}$

c)$y'\left(x\right)=e^x.2sinxcosx+e^xsin^2x.2cosx$

$=2e^xsinx\left(cosx+sinxcosx\right)$

$=2e^xsinxcos^2x$

d)$y'\left(x\right)=\dfrac{1}{x\sqrt{x}}.\left(+\dfrac{1}{2\sqrt{x}}\right)$

$=\dfrac{1}{\sqrt{x}\left(2\sqrt{x}+\sqrt{x}+2\right)}$

$=\dfrac{1}{\sqrt{x}\left(3\sqrt{x}+2\right)}$

Đúng(1)

B

Buddy

13 tháng 8 2023

Tìm đạo hàm của mỗi hàm số sau:

a) $y = 4{x^3} - 3{x^2} + 2x + 10$

b) $y = \frac{{x + 1}}{{x - 1}}$

c) $y = - 2x\sqrt x $

d) $y = 3\sin x + 4\cos x - \tan x$

e) $y = {4^x} + 2{e^x}$

f) $y = x\ln x$

#Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

14 tháng 8 2023

a: $y'=4\cdot3x^2-3\cdot2x+2=12x^2-6x+2$

b: $y'=\dfrac{\left(x+1\right)'\left(x-1\right)-\left(x+1\right)\left(x-1\right)'}{\left(x-1\right)^2}=\dfrac{x-1-x-1}{\left(x-1\right)^2}=\dfrac{-2}{\left(x-1\right)^2}$

c: $y'=-2\cdot\left(\sqrt{x}\cdot x\right)'$

$=-2\cdot\left(\dfrac{x+x}{2\sqrt{x}}\right)=-2\cdot\dfrac{2x}{2\sqrt{x}}=-2\sqrt{x}$

d: $y'=\left(3sinx+4cosx-tanx\right)$'

$=3cosx-4sinx+\dfrac{1}{cos^2x}$

e: $y'=\left(4^x+2e^x\right)'$

$=4^x\cdot ln4+2\cdot e^x$

f: $y'=\left(x\cdot lnx\right)'=lnx+1$

Đúng(1)

B

Buddy

17 tháng 8 2023

Tính đạo hàm cấp hai của các hàm số sau:

a) $y = x{e^{2x}};$

b) $y = \ln \left( {2x + 3} \right).$

#Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

17 tháng 8 2023

a: $y=x\cdot e^{2x}$

=>$y'=\left(x\cdot e^{2x}\right)'$

$=x\cdot\left(e^{2x}\right)'+x'\cdot\left(e^{2x}\right)$

$=e^{2x}+2\cdot x\cdot e^{2x}$

$y''=\left(e^{2x}+2\cdot x\cdot e^{2x}\right)'$

$=\left(e^{2x}\right)'+\left(2\cdot x\cdot e^{2x}\right)'$

$=4\cdot e^{2x}+4\cdot x\cdot e^{2x}$

b: $y=ln\left(2x+3\right)$

=>$y'=\dfrac{\left(2x+3\right)'}{\left(2x+3\right)}=\dfrac{2}{2x+3}$

=>$y''=\left(\dfrac{2}{2x+3}\right)'=\dfrac{2\left(2x+3\right)'-2'\left(2x+3\right)}{\left(2x+3\right)^2}$

$=\dfrac{4}{\left(2x+3\right)^2}$

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP