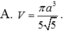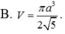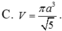Cho tứ diện ABCD có DA vuông góc với mặt phẳng (ABC), DB vuông góc BC, AD = AB = BC = a. Kí hiệu V 1 , V 2 , V 3 lần lượt là thể tích của hình tròn xoay sinh bởi tam giác ABD khi quay quanh AD, tam giác ABC khi quay quanh AB, tam giác DBC khi quay quanh BC. Trong các mệnh đề sau, mệnh đề nào đúng?
A. V 1 = V 2 = V 3
B. V 1 + V 2 = V 3
C. V 1 = V 2 + V 3
D. V 1 + V 3 = V 2