Trong hệ trục tọa độ Oxyz cho mặt phẳng (P): y + 2z = 0; điểm A(1;2;3), B(-1,1,1). Tìm tổng tọa độ của điểm M trên (P) sao cho chu vi tam giác MAB đạt giá trị bé nhất.
A. − 14 55
B. 2 5
C. − 1 5
D. − 17 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương trình đường thẳng qua M và vuông góc với (P)x-y+2z-3=0 là:
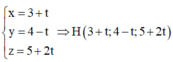
![]()
![]()

Đáp án B
Phương trình đường thẳng qua M và vuông góc với (P): x – y + 2z – 3 = 0 là:
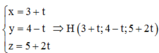
![]()
![]()

Chọn B
Phương trình đường thẳng Δ đi qua M và vuông góc với mặt phẳng (P) là 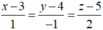 .
.
Tọa độ H là hình chiếu vuông góc của M lên mặt phẳng (P) là nghiệm của hệ phương trình:
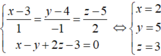
Vậy H (2; 5; 3)

Chọn B

Gọi A là một điểm thuộc d => tọa độ của A thỏa mãn HPT

Đáp án A
Điều này xảy ra khi và chỉ khi M là giao điểm của A'B với (P) (Với A' là điểm đối xứng của A qua (P)).
Dựa vào yếu tố vuông góc và trung điểm ta tính được A ' 1 ; − 6 5 ; − 17 5