Cho tứ diện SABC có trọng tâm G. Một mặt phẳng qua G cắt các tia SA, SB và SC theo thứ tự tại A’, B’ và C’. Đặt S A ' S A = m ; S B ' S B = n ; S C ' S C = p .Đẳng thức nào dưới đây là đúng
A. 1 m 2 + 1 n 2 + 1 p 2 = 4
B. 1 m n + 1 n p + 1 p m = 4
C. 1 m + 1 n + 1 p = 4
D. m + n + p = 4

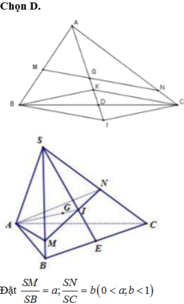

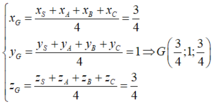
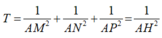
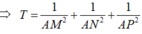
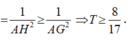



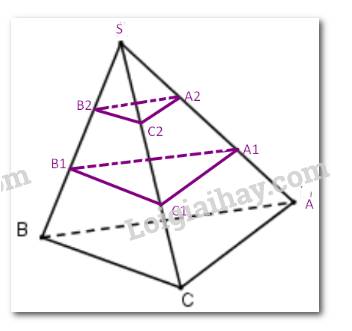
Gọi G 1 là trọng tâm của tam giác ABC. Khi đó
So sánh hai đẳng thức trên ta suy ra
Nhưng do S A → ; S B → ; S C → là ba vecto không đồng phẳng nên đẳng thức trên xảy ra khi và chỉ khi
Từ đây và do x + y + z = 1 ta thu được 1 m + 1 n + 1 p = 4
Chọn C.
n