Cho hàm số y = f(x) liên tục trên R, có đồ thị như hình vẽ. Các giá trị của tham số m để phương trình 4 m 3 + m 2 f 2 ( x ) + 5 = f 2 ( x ) + 3 có ba nghiệm phân biệt là
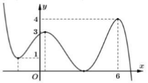
A. m = ± 37 2
B. m = 3 2
C. m = - 37 2
D. m = 37 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TH1: Với x- 1≥0 hay x≥ 1
khi đó f(x) |x - 1| = m <=> m = f(x).(x - 1) (1)
Dựa vào đồ thị ( C) trên khoảng [1; +∞] để (1) có 2 nghiệm khi và chỉ khi -0,6< m≤0
TH2: Với x< 1 khi đó f(x)|x-1| = m <=> -m = f(x).(x-1) (2)
Dựa vào đồ thị (C) trên khoảng ( - ∞ ; - 1 ) để (1) có 3 nghiệm
Khi và chỉ khi 0≤ -m <0,7 hay – 0,7< m ≤0
Kết hợp 2 TH, ta thấy -0,6<m< 0 thì phương trình có tối đa 5 nghiệm ( m= 0 loại vì phương trình có 4 nghiệm).
Chọn B.

Chọn đáp án B
Phương pháp
+) Đặt t=cosx, xác định khoảng giá trị của t, khi đó phương trình trở thành f(t)=m.
+) Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f(t) và y=m song song với trục hoành.
Cách giải
Đặt t=cosx ta có
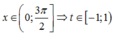
Khi đó phương trình trở thành f(t)=m.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f(t) và y=m song song với trục hoành.
Dựa vào đồ thị hàm số y=f(x) ta thấy phương trình f(t)=m có 2 nghiệm phân biệt thuộc [-1;1) khi và chỉ khi mÎ(0;2).

Đáp án D
Phương pháp:
Số nghiệm của phương trình |f(x)| = m bằng số giao điểm của đồ thị hàm số y = |f(x)| và đường thẳng y = m
Cách giải:
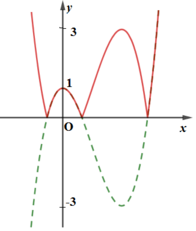
Từ đồ thị hàm số y = f(x) ta có đồ thị hàm số y = |f(x)| như hình bên:
Số nghiệm của phương trình |f(x)| = m bằng số giao điểm của đồ thị hàm số y = |f(x)| và đường thẳng y = m
⇒ Để phương trình |f(x)| = m có 4 nghiệm phân biệt thì 1 < m < 3

Chọn đáp án D.
![]()
Do đó để phương trình f sin x = m có nghiệm trong khoảng (0;p)
thì phương trình f t = m có nghiệm t ∈ ( 0 ; 1 ]

Đặt t=2sinx+1 với
![]()
![]()
![]()
Phương trình trở thành: f(t)=m có nghiệm ![]()
Chọn đáp án A.
Chọn C.