Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a cạnh bên SA vuông góc
mặt đáy và SA = a . Gọi φ là góc tạo bởi SB và mặt (ABCD). Xác định cot φ
A. cot φ = 2
B. cot φ = 1 2
C. cot φ = 2 2
D. cot φ = 2 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có: B là hình chiếu của B lên (ABCD)
A là hình chiếu của S lên (ABCD)
Suy ra góc tạo bởi (ABCD) là góc φ = S B A ^ .
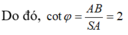

a) Ta có:
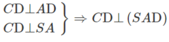
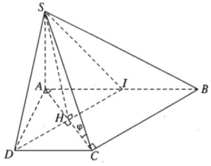
⇒ (SCD) ⊥ (SAD)
Gọi I là trung điểm của đoạn AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì DI // CB và DI ⊥ CA nên AC ⊥ CB. Do đó CB ⊥ (SAC).
Vậy (SBC) ⊥ (SAC).
b) Ta có:
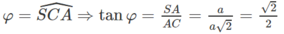
c) 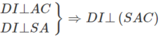
Vậy (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI). Do đó thiết diện của (α) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng a√2. Gọi H là tâm hình vuông AICD ta có SH ⊥ DI và 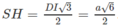 .
.
Tam giác SDI có diện tích:
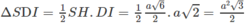

Đáp án A.
* Hướng dẫn giải:
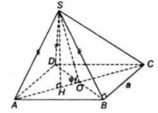
Dễ thấy AB = BC và A B C ⏜ = 60 o nên tam giác ABC đều.
Gọi H là hình chiếu của A lên (ABCD).
Do SA = SB =SC nên H là tâm đường tròn ngoại tiếp tam giác ABC.
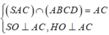
![]()
Mặt khác, H O = 1 3 B O = 1 3 . a 3 2 = a 3 6
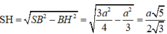
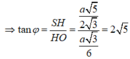

a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)
=> Tam giác ABD cân tại A. Lại có góc A= 60o
=> Tam giác ABD đều.
Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.
* Gọi H là tâm của tam giác ABD
=>SH ⊥ (ABD)
*Gọi O là giao điểm của AC và BD.
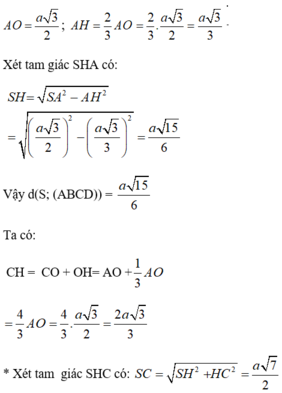

Đáp án A
Ta có: B là hình chiếu của B lên (ABCD) .