Cho hàm số y=f(x) xác định trên M và có đạo hàm f ' x = x + 2 x - 1 2 Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số y=f(x)đồng biến trên (-2;+∞)
B. Hàm số y=f(x)đạt cực đại tại x= -2
C. Hàm số y=f(x)đạt cực đại tiểu x=1
D. Hàm số y=f(x)nghịch biến trên (-2;1)

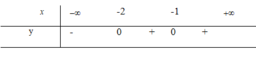
Ta lập bảng xét dấu của y’
x
+∞ -2 -1 +∞
y’
- 0 + 0 +
Từ bảng xét dấu trên thì hàm số đồng biến trên (-2;+∞)
Đáp án A