Hàm số f x = 2 s i n x + s i n 2 x trên đoạn 0 ; 3 π 2 có giá trị lớn nhất là M, giá trị nhỏ nhất là m Khi đó M+m bằng:
A. − 3 3
B. 3 3
C. − 3 3 4
D. 3 3 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Xét I = ∫ 0 1 f ' x d x Đặt t = x → t 2 = x → 2 t d t = d x
Đổi cận x = 0 → t = 0 x = 1 → t = 1 . Khi đó I = 2 ∫ 0 1 t f ' ( t ) d t = 2 A
Tính A = ∫ 0 1 t f ' ( t ) d t . Đặt u = t d v = f ' t d t → d u = d t v = f t
Khi đó
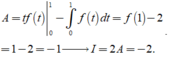

Đáp án A
Ta có - 1 30 = ∫ 1 2 x - 1 f ( x ) d x = 1 2 ∫ 1 2 f ( x ) d x - 1 2
= 1 2 x - 1 2 f ( x ) 1 2 - 1 2 ∫ 1 2 x - 1 2 f ' x d x
⇔ ∫ 1 2 x - 1 2 f ' ( x ) d x = 1 15
Ta lại có ∫ 1 2 x - 1 4 d x = 1 5 x - 1 5 1 2 = 1 5
Từ giả thiết và các kết quả ta có
9 ∫ 1 2 f ' ( x ) 2 d x - 6 ∫ 1 2 x - 1 2 f ' ( x ) d x + ∫ 1 2 x - 1 4 d x = 0
Mặt khác:
9 ∫ 1 2 f ' ( x ) 2 d x - 6 ∫ 1 2 x - 1 2 f ' ( x ) d x + ∫ 1 2 x - 1 4 d x = ∫ 1 2 3 f ' ( x ) - x - 1 2 2
Do vậy xét trên đoạn [1;2] , ta có
3 f ' ( x ) - ( x - 1 ) 2 = 0 ⇔ f ' ( x ) = 1 3 x - 1 2 ⇒ f ( x ) = 1 9 x - 1 3 + c
Lại do f(2) = 0 nên C + 1 9 = 0 ⇔ C = - 1 9 ⇒ f ( x ) = 1 9 x - 1 3 - 1 9
Suy ra I = 1 9 ∫ 1 2 x - 1 3 - 1 d x = 1 36 x - 1 4 1 2 - 1 9 x - 1 1 2 = - 1 12

Đáp án là C
Câu III sai vì thiếu dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I
Câu IV sai vì có thể vô số điểm trên I xuất hiện rời rạc thì vẫn có thể nghịch biến trên khoảng I
Đáp án D
f ' x = 2 cos x + 2 cos 2 x = 2 cos x + 4 cos 2 x − 2.
f ' x = 0 ⇔ cos x = − 1 cos x = 1 2 ⇔ x = π + k 2 π x = ± π 3 + k 2 π k ∈ ℤ .
=>M= 3 3 2 , m=0