Cho hàm y = x 2 = m x + 2 x - 1 . Có bao nhiêu giá trị nguyên dương của m ∈ 0 ; 2019 thỏa mãn hàm số đồng biến trên các khoảng - ∞ ; 1 , 1 ; + ∞ biết m
A. 672
B. 673
C. 674
D. 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số g(x) nghịch biến trên khoảng (0;1) khi ![]()
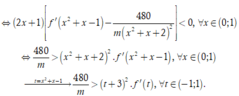
Dựa vào đồ thị, ta có
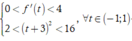
![]()
Theo YCBT 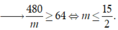
Chọn C.

Đáp án D
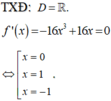
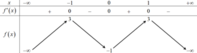
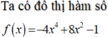
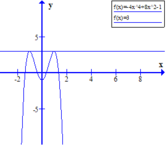
Dựa vào đồ thị suy ra có một giá trị nguyên dương của m để phương trình f(x)=m có đúng hai nghiệm phân biệt là m=3.
y = x 2 = m x + 2 x - 1 = y ' = 2 x - m x - 1 - x 2 - m x + 2 x - 1 2
= x 2 - 2 x + m - 2 x - 1 2
Để hàm số đồng biến trên tập xác định của nó thì
∆ = 1 - m + 2 = 3 - m ≤ 0 ⇒ m ≥ 3
Như vậy số các giá trị m thỏa mãn ĐK là
2019 - 3 3 + 1 = 673
Đáp án cần chọn là B