Thí nghiệm giao thoa ánh sáng bằng khe Y–âng thực hiện đồng thời với ba bức xạ đỏ, lục và lam có bước sóng lần lượt là: λ1 = 0,72 μm, λ2 = 0,54 μm và λ3 = 0,48 μm. Vân sáng đầu tiên kể từ vân sáng trung tâm có cùng màu với vân sáng trung tâm ứng với vị trí vân sáng bậc mấy của vân sáng màu đỏ?
A. 6.
B. 8.
C. 9.
D. 4.

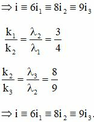


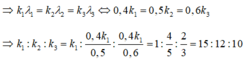
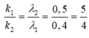
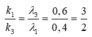
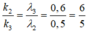



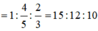
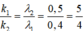
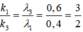
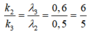


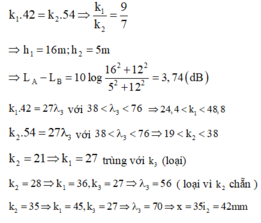
Đáp án A