Biết đồ thị hàm số y = 2 m - n x 2 + m x + 1 x 2 + m x + n - 6 (m, n là tham số) nhận trục hoành và trục tung làm hai đường tiệm cận. Tính m + n
A.-6
B.9
C.6
D.8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Vì hai đồ thị cắt nhau tại một điểm trên trục tung nên n=-4
=>m=-2

a: 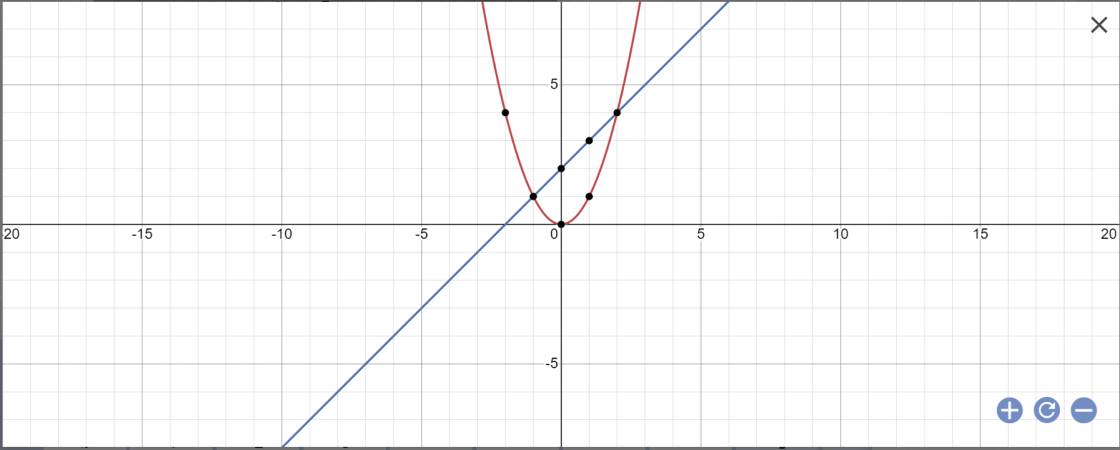
PTHĐGĐ là:
x^2-x-2=0
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
Khi x=-1 thì y=(-1)^2=1
Khi x=2 thì y=2^2=4
b: Để y=(m-1)x+m+n trùng với y=-2x+1 thì
m-1=-2 và m+n=1
=>m=-1 và n=1-m=1-(-1)=2

Đáp án A
Để đồ thị hàm số y = (2m + 1)x + n trùng với đường thẳng y = 3x - 2 thì:
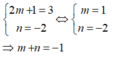

Câu 2:
a) Để đồ thị hàm số \(y=\left(m+1\right)x^2\) đi qua điểm A(1;2) thì
Thay x=1 và y=2 vào hàm số \(y=\left(m+1\right)x^2\), ta được:
m+1=2
hay m=1
Vậy: m=1

a: Thay x=-2 và y=-2 vào (d1), ta đc:
-2(2m+1)+m-3=-2
=>-4m-2+m-3=-2
=>-3m-5=-2
=>-3m=3
=>m=-1
b: Tọa độ giao của (d2) với trục hoành là:
y=0 và (2a+1)x+4a-3=0
=>x=-4a+3/2a+1
Để x nguyên thì -4a-2+5 chia hết cho 2a+1
=>\(2a+1\in\left\{1;-1;5;-5\right\}\)
=>\(a\in\left\{0;-1;2;-3\right\}\)

\(A\left(2;-6\right)\inđths\Leftrightarrow2m-2=-6\Leftrightarrow m=-2\)