Biết số nguyên tố a b c có các chữ số theo thứ tự lần lượt lập thành cấp số nhân. Giá trị a 2 + b 2 + c 2 là
A. 20
B. 21
C. 15
D. 17
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 10 2017
Đáp án B
Từ giả thiết ta có
b 2 = a c a + c = 2 ( b + 8 ) b + 8 2 = a ( c + 64 ) ⇔ b 2 = a c a + c = 2 ( b + 8 ) b + 8 2 = b 2 + 64 a ⇔ b 2 = a c c = 7 a + 8 b = 4 a − 4
⇔ 4 a - 4 2 = a 7 a + 8 c = 7 a + 8 b = 4 a - 4 ⇔ 9 a 2 - 40 a + 16 = 0 c = 7 a + 8 b = 4 a - 4 ⇔ a = 4 ; b = 12 ; c = 36 a = 4 9 ; b = - 20 9 ; c = 100 9
Do a,b,c tạo thành một dãy số tăng nên a = 4 ; b = 12 ; c = 36 .
Suy ra
a − b + 2 c = 4 − 12 + 2.36 = 64.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
Ba số \(\frac{2}{{b - a}},\frac{1}{b},\frac{2}{{b - c}}\) theo thứ tự lập thành cấp số cộng nên ta có:
\(\begin{array}{l}\frac{2}{{b - a}} + \frac{2}{{b - c}} = 2.\frac{1}{b} \Leftrightarrow \frac{1}{{b - a}} + \frac{1}{{b - c}} = \frac{1}{b} \Leftrightarrow \frac{{\left( {b - c} \right) + \left( {b - a} \right)}}{{\left( {b - a} \right)\left( {b - c} \right)}} = \frac{1}{b}\\ \Leftrightarrow \frac{{b - c + b - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow \frac{{2b - c - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow b\left( {2b - c - {\rm{a}}} \right) = {b^2} - ab - bc + ac\\ \Leftrightarrow 2{b^2} - bc - {\rm{ab}} = {b^2} - ab - bc + ac \Leftrightarrow {b^2} = {\rm{a}}c\end{array}\).
Vậy ba số \(a,b,c\) theo thứ tự lập thành cấp số nhân.
CM
1 tháng 8 2017
Chọn D
Theo tính chất cấp số nhân, Ta có: ac=2/3 b2. Theo hệ thức lượng trong tam giác vuông, Ta có: b=a.sinB, c=a.cosB. vậy Ta có
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 1 2021
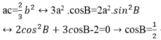
Do 3 số lập thành 1 CSC nên: \(2\left(a+8\right)=1+b\Rightarrow b=2a+15\)
Do 3 số lập thành 1 CSN nên:
\(a^2=b.1\Leftrightarrow a^2=2a+15\)
\(\Leftrightarrow a^2-2a-15=0\Rightarrow\left[{}\begin{matrix}a=5\\b=-3< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow b=2a+15=25\)
Đáp án B
Số đó là 421, đây là số nguyên tố (chỉ chia hết cho 1 và chính nó)
Ta thấy 4, 2, 1 theo thứ tự lần lượt lập thành cấp số nhân có công bội q = 1 2
Giá trị a 2 + b 2 + c 2 là 21