Trong hông gian Oxyz , cho điểm A(-3;-4;10). Có bao nhiêu đường thẳng qua A cắt mặt phẳng (Oxy) tại điểm M và cắt trục Oz tại điểm N sao cho tam giác OMN vuông cân ?
A. 3
B. 0
C. 2
D. 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có điểm tiếp xúc là h/c(A,(Oxyz))=N(0;-1;1)
Chọn đáp án B.

Đáp án B
Phương pháp:
Hai vectơ
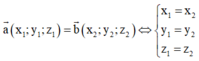
Cách giải:
Gọi điểm B x 0 ; y 0 ; z 0 là điểm cần tìm. Khi đó
![]()
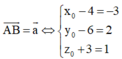
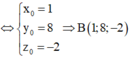

Đáp án B
Gọi N là hình chiếu của A(3;-1;1) lên (Oyz) => N(0;-1;1)

Hình chiếu vuông góc của A ( 3;-1;1 ) lên Oyz là điểm N thuộc mặt phẳng Oyz nen x = 0.
Vậy hình chiếu của A ( 3;-1;1 ) lên Oyz là N ( 0;-1;1 )
Đáp án cần chọn là B

Đáp án B.
Gọi N là hình chiếu của A(3;-1;1) lên (Oyz) ⇒ N(0;-1;1).

Đáp án C
Do A' đối xứng với A qua H nên AA' nhận H làm trung điểm
=> xA' = 2xH-xA = 1; yA' = 2yH-yA = -7; zA' = 2zH-zA = -5.
Ta có
Vậy điều kiện tam giác OMN vuông cân là OM = ON > 0.
Gọi M(a;b;0), N(0;0;c)(c#0)
Do ba điểm A, M, N thẳng hàng nên A M ⇀ = k A N ⇀
Suy ra (k#1,k#0)
(k#1,k#0)
Có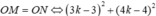
Đối chiếu điều kiện nhận k = ± 2
Vậy có hai đường thẳng thoả mãn.
Chọn đáp án C.