Cho cấp số nhân u n có u 1 = 2 và biểu thức 20 u 1 - 10 u 2 + u 3 đạt giá trị nhỏ nhất. Số hạng thứ bảy của cấp số nhân u n có giá trị bằng
A. 31250
B. 6250
C. 136250
D. 39062
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

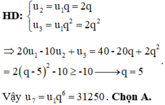


Câu 1:
Ta thấy:
\(\left(x-\frac{2}{5}\right)^2\ge0\Rightarrow\frac{1}{3}\cdot\left(x-\frac{2}{5}\right)^2\ge0\)
\(\left|2y+1\right|\ge0\)
\(\Rightarrow\frac{1}{3}\cdot\left(x-\frac{2}{5}\right)^2+\left|2y+1\right|\ge0\)
\(\Rightarrow\frac{1}{3}\cdot\left(x-\frac{2}{5}\right)^2+\left|2y+1\right|-2,5\ge-2,5\)
hay \(A\ge-2,5\)
Dấu "=" xảy ra khi \(\begin{cases}\left(x-\frac{2}{5}\right)^2=0\\\left|2y+1\right|=0\end{cases}\)
\(\Rightarrow\begin{cases}x-\frac{2}{5}=0\\2y+1=0\end{cases}\)
\(\Rightarrow\begin{cases}x=\frac{2}{5}\\2y=-1\end{cases}\)
\(\Rightarrow\begin{cases}x=\frac{2}{5}\\y=-\frac{1}{2}\end{cases}\)
Vậy GTNN của A là -2,5 đạt được khi \(\begin{cases}x=\frac{2}{5}\\y=-\frac{1}{2}\end{cases}\)

Chọn A
Gọi q là công bội của cấp số nhân (un)
Ta có: u1 = 3; u2 = 3q; u3 = 3q2
⇒ 15 u 1 − 4 u 2 + u 3 = 15.3 − 4.3 q + 3 q 2 = 45 − 12 q + 3 q 2 = 3 q − 2 2 + 33 ≥ 33 ∀ q .
Suy ra 15 u 1 − 4 u 2 + u 3 đạt GTNN khi q = 2 .
Khi đó u 13 = u 1 q 12 = 12288.

Chọn B.
Gọi q là công bội của cấp số nhân (un)
Ta có 15u1 – 4u2 + u3 = 45 – 12q + 3q2 = 3(q – 2)2 + 33 ≥ 33 ∀ q
⇒ min(15u1 – 4u2 + u3) = 33 khi q = 2
Suy ra u13 = u1q12 = 3.212 = 12288.