Số có giá trị nguyên của tham số m thuộc đoạn - 2019 ; 2 để phương trình x - 1 log 3 4 x + 1 + log 5 2 x + 1 = 2 x - m có đúng hai nghiệm thực là
A. 2021
C. 1
C. 2
D. 2022
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

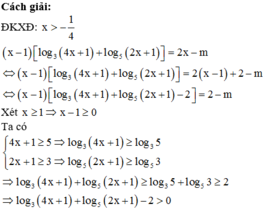
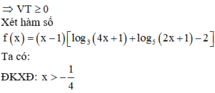
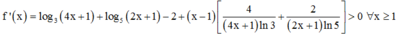
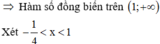
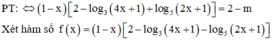
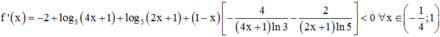

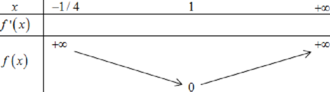


Chọn A.
TXĐ: D = R
Ta có: y ' = 3 x 2 - 6 x + 3 m
Để hàm số đã cho nghịch biến trên 1 ; 2
thì y ' ≤ 0 , ∀ x ∈ 1 ; 2 và bằng 0 tại hữu hạn điểm
![]()
![]()
![]()
![]()
Hàm số y = x - 1 2 đồng biến trên 1 ; + ∞ nên cũng đồng biến trên 1 ; 2
![]()
![]()
Lại có m ∈ - 10 ; 10 và m ∈ Z nên m ∈ - 10 ; - 9 ; . . ; 0
Vậy có 11 giá trị của m

Có ![]()
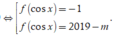
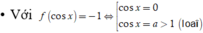
![]()
Phương trình này có hai nghiệm ![]()
• Với ![]() ta cần tìm điều kiện để phương trình này có 4 nghiệm phân biệt thuộc
ta cần tìm điều kiện để phương trình này có 4 nghiệm phân biệt thuộc ![]()
![]()
![]()
Với t = -1 phương trình (1) cho đúng một nghiệm x =
π
; với t = 0 phương trình cho hai nghiệm ![]()
Với mỗi ![]() phương trình cho hai nghiệm thuộc
phương trình cho hai nghiệm thuộc![]()
Vậy điều kiện cần tìm là phương trình (1) phải có hai nghiệm phân biệt
![]()
![]()
Chọn B.

Đáp án D
P T ⇔ m + 1 1 − c os 2 x 2 − sin 2 x + cos 2 x = 0 ⇔ sin 2 x + m − 1 2 c os 2 x = m + 1 2 .
PT có nghiệm ⇔ 1 2 + m − 1 2 2 ≥ m + 1 2 2 ⇔ m ≤ 1.
Vì m ∈ − 2018 ; 2018 ⇒ có 2020 giá trị nguyên của m.