Cho a,b là các số thực dương thỏa mãn a 2 + b 2 = 14 a b . Khẳng định nào sau đây sai?
A. 2 log 2 a + b = 4 + log 2 a + log 2 b .
B. ln a + b 4 = ln a + ln b 2 .
C. 2 log a + b 4 = log a + log b .
D. 2 log 4 a + b = 4 + log 4 a + log 4 b .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Cho 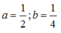 ta thấy logab= 2 và logba= ½. Do vậy logba< 1< logab
ta thấy logab= 2 và logba= ½. Do vậy logba< 1< logab

Chọn D
Cách 1: Cho a= 4; b= 2 ta thấy log24> 1> log42
Cách 2: Ta có: 1< a< b nên


\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B

Ta có: a – b = 2 nên a= b +2.
Khi đó; tích a b = b + 2 . b = b 2 + 2 b = b 2 + 2 b + 1 - 1 = b + 1 2 - 1 ≥ - 1 ∀ b
Vậy tích ab nhỏ nhất là -1 khi b = -1 ; a= 1

Đáp án D.