Họ nguyên hàm F(x) của hàm số f ( x ) = 2 − ln 2 ( 2 x + 1 ) 2 x + 1 là
A. F ( x ) = ln 2 x + 1 − ln 3 2 x + 1 6 + C
B. F ( x ) = − 2 + 2 ln 2 x + 1 2 x + 1 2 + C
C. F ( x ) = 2 ln ( 2 x + 1 ) − ln 3 2 x + 1 3 + C
D. F ( x ) = 2 ( 2 x + 1 ) − ln 3 2 x + 1 + C


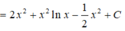
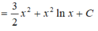
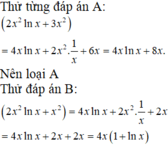
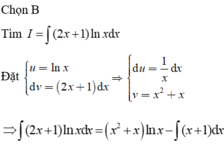
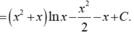
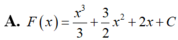
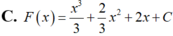
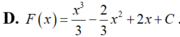

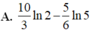
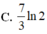
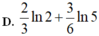


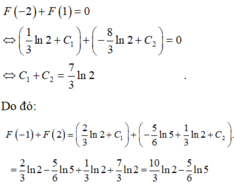
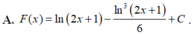
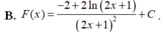
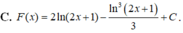
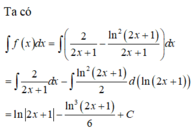
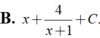
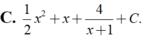
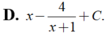
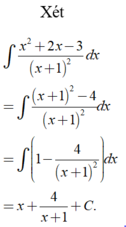
Đáp án A
Ta có