Cho tam giác ABC có các góc A, B, C tạo thành một cấp số nhân công bội 2. Khẳng định nào sau đây đúng
A. 1 a = 1 b + 1 c
B. 1 b = 1 a + 1 c
C. 1 c = 1 b + 1 a
D. 1 a + 1 b + 1 c = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

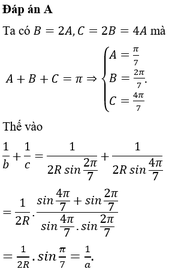

Xét cấp số nhân a, aq, a q 2 , a q 3
Suy ra có dãy số
log a , log a + log q log a + 2 log q log a + 3 log q
Đây là cấp số cộng với công sai d = log q > 0
Đáp án cần chọn là C

Ta có A B → = 2 ; 2 , B C → = 0 ; − 4 và A C → = 2 ; − 2 .
Suy ra A B = A C = 2 2 A B 2 + A C 2 = B C 2 .
Vậy tam giác ABC vuông cân tại A.
Chọn D

\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp AH\)
Mà \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp SC\)
Các khẳng định đúng là (1) và (2)

Đáp án D
Ta có thể thấy ngay rằng các khẳng định A và C đều đúng.
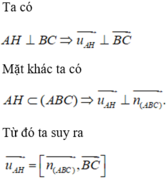
là một vectơ chỉ phương của đường thẳng AH.
Vậy D là khẳng định sai.

A(1; 4), B(3; -2), C(4; 5)
Thay lần lượt tọa độ các đỉnh vào biểu thức P(x,y)= 2x – 5y + 3 ta có
P(1,4) = 2.1 – 5.4 + 3 = – 15, P(3, –2) = 2.3 – 5.( –2) + 3 = 19
P(4,5) = 2.4 – 5.5 + 3 = – 14
Do đó đường thẳng ∆ cắt các cạnh AB, BC và không cắt cạnh AC.
Đáp án C