Chứng tỏ rằng tổng của một số nhỏ hơn 0 với nghịch đảo của nó thì ko lon hơn 2
Làm ơn giúp mình đi mà thank
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DH
3
NN
26 tháng 3 2019
Gọi 2 số nghịch đảo nhau là a/b và b/a (a,b > 0)
Theo đề bài ta cần chứng minh a/b +b/a lớn hơn hoặc bằng 2
Không mất tính tổng quát, giả sử a lớn hơn hoặc bằng b, suy ra a = b + m (m lớn hơn hoặc bằng 0)
Ta có: a/b + b/a = (b+m)/b + b/(b+m) = 1 + m/b + b/(b+m)
\(\frac{a}{b}+\frac{b}{a}=\frac{b+m}{b}+\frac{b}{b+m}=1+\frac{m}{b}+\frac{b}{b+m}\)
NN
26 tháng 3 2019
\(\ge1+\frac{m}{b+m}+\frac{b}{b+m}=1+\frac{m+b}{b+m}=1+1=2\)
Vậy a/b + b/a lớn hơn hoặc bằng 2 (điều phải chứng minh)
NX
0
NK
1
NX
1
AH
Akai Haruma
Giáo viên
4 tháng 10
** Sửa đề: Tổng của 1 số nhỏ hơn 0 với nghịch đảo của nó thì không lớn hơn 2.
Lời giải:
Gọi số nhỏ hơn $0$ là $a$. Nghịch đảo của nó là $\frac{1}{a}$
Xét hiệu: $a+\frac{1}{a}-2=\frac{a^2-2a+1}{a}=\frac{(a-1)^2}{a}$
Ta thấy: $(a-1)^2\geq 0$ với mọi $a<0$
$a<0$
$\Rightarrow \frac{(a-1)^2}{a}\leq 0$
$\Rightarrow a+\frac{1}{a}-2\leq 0$
$\Rightarrow a+\frac{1}{a}\leq 2$
Vậy ta có đpcm.
TP
0
CM
2 tháng 9 2019
Gọi a/b với a > 0, b > 0 là phân số đã cho và b/a là phân số nghịch đảo của nó . Không mất tính tổng quát giả sử 0 < a ≤ b.
Đặt b = a + m (m ∈ Z, m ≥ 0)
Ta có:
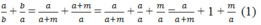
Và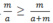 
(dấu "=" xảy ra khi m = 0)
Suy ra: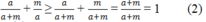 
Từ (1) và (2) suy ra:
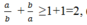, (dấu "=" xảy ra khi m = 0 hay a = b )
KT
1
NT
1
2 tháng 3 2017
Giả sử phân số và nghịch đảo của nó là: \(\frac{a}{b};\frac{b}{a}\)
Do phân số dương nên( a;b) cùng dấu hay a.b>0
Ta có:
\(\frac{a}{b}+\frac{b}{a}-2=\frac{a^2+b^2-2ab}{ab}=\frac{\left(a-b\right)^2}{ab}\ge0\)
Do đó: \(\frac{a}{b}+\frac{b}{a}\ge2\)
ML
10 tháng 6 2015
Giả sử phân số và nghịch đảo của nó là \(\frac{a}{b};\frac{b}{a}\)
Do phân số dương nên \(a;b\)cùng dấu hay \(a.b>0\)
Ta có \(\frac{a}{b}+\frac{b}{a}-2=\frac{a^2+b^2-2ab}{ab}=\frac{\left(a-b\right)^2}{ab}\ge0\)
Do đó \(\frac{a}{b}+\frac{b}{a}\ge2\)
Lời giải:
Gọi số nhỏ hơn $0$ là $a$. Nghịch đảo của nó là $\frac{1}{a}$
Xét hiệu: $a+\frac{1}{a}-2=\frac{a^2-2a+1}{a}=\frac{(a-1)^2}{a}$
Ta thấy: $(a-1)^2\geq 0$ với mọi $a<0$
$a<0$
$\Rightarrow \frac{(a-1)^2}{a}\leq 0$
$\Rightarrow a+\frac{1}{a}-2\leq 0$
$\Rightarrow a+\frac{1}{a}\leq 2$
Vậy ta có đpcm.