Cho hình hộp ABCD.A’B’C’D’. Trên các cạnh AA’, BB’, CC’ lần lượt lấy ba điểm M, N, P sao cho A ' M A A ' = 1 3 , B ' N B B ' = 2 3 , C ' P C C ' = 1 2 . Biết mặt phẳng (MNP) cắt cạnh DD’ tại Q. Tính tỉ số D ' Q D D '
A. 1 6
B. 1 3
C. 5 6
D. 2 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
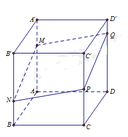
Ta chứng minh được công thức tỷ số thể tích tối với khối hộp như sau (học sinh có thể tự chứng minh).
V A ' B ' C ' D ' . M N P Q V A " B ' C ' D ' . A B C D = 1 2 A ' M A ' A + C ' P C ' C = 1 2 B ' N B ' B + D Q D ' D
Khi đó: 1 3 + 1 2 = 2 3 + D Q D ' D ⇔ D Q D ' D = 1 6 .

Đáp án A
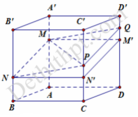
Lấy M’, N’ lần lượt trên các cạnh DD’ và CC’ sao cho M A = M ' D và N B = N ' C .
Vì A B B ' A ' / / C DD ' C ' nên 2 giao tuyến giữa mặt phẳng (MNP) lần lượt với các mặt phẳng (ABB'A') và (CDC'C') sẽ song song với nhau. Do vậy ta sẽ lấy Q ∈ DD ' sao cho M N / / P Q . Ta có:
D Q ' = D ' M ' − Q M ' = DD ' 3 − P C − N ' C = DD ' 3 − DD ' 2 − DD ' 3 = DD ' 6 ⇒ D ' Q DD ' = 1 6 .