Cho hàm số f(x) có f ' x ≤ 0 ∀ x ∈ ℝ và f '(x) thì chỉ tại một số hữu hạn điểm thuộc R. Hỏi khẳng định nào sau đây là khẳng định đúng?
A. Với mọi x 1 , x 2 ∈ ℝ và x 1 ≠ x 2 , ta có f x 1 − f x 2 x 1 − x 2 < 0 .
B. Với mọi x 1 , x 2 ∈ ℝ và x 1 ≠ x 2 , ta có f x 1 − f x 2 x 1 − x 2 > 0 .
C. Với mọi x 1 , x 2 , x 3 ∈ ℝ và x 1 < x 2 < x 3 , ta có f x 3 − f x 2 f x 3 − f x 1 < 0 .
D. Với mọi x 1 , x 2 , x 3 ∈ ℝ và x 1 < x 2 < x 3 , ta có f x 1 − f x 2 f x 2 − f x 3 < 0

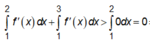
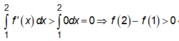
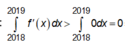

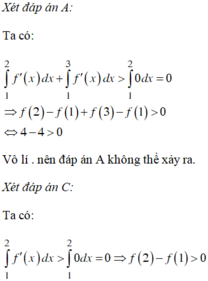







Đáp án A.
Cho hàm số f(x) có f ' x ≤ 0 ∀ x ∈ ℝ và f '(x) = 0 chỉ tại một số hữu hạn điểm thuộc R. Nên Hàm số f(x) nghịch biến trên R nên ∀ x 1 , x 2 ∈ K ; x 1 < x 2 ⇔ f x 1 > f x 2
Ta có x 1 − x 2 < 0 ; và f x 1 − f x 2 > 0 ⇒ f x 1 − f x 2 x 1 − x 2 < 0