Cho các số phức z 1 , z 2 thỏa mãn z 1 = 3 , z 2 = 4 và z 1 - z 2 = 5 . Gọi A, B lần lượt là điểm biểu diễn các số phức z 1 , z 2 . Diện tích S của tam giác OAB với O là gốc tọa độ là:
A. S = 25 2
B. S = 5 2
C. S=6
D. S=12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn C.
Đặt z = a+ bi.
Theo đề ra ta có: ( 3 + i) z = 2
Hay ( 3 + i)( a + bi) = 2
Suy ra: 3a - b + ( 3b + a) i = 2
![]()
nên z = 3/5 - 1/5i.
Khi đó w = 3/5 - 1/5i + 2/5 - 4/5 i = 1 - i.
Vậy ![]()

Đáp án C
HD: Ta có
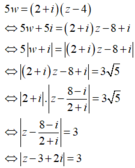
![]() Tập hợp điểm M(z) là đường tròn
Tập hợp điểm M(z) là đường tròn ![]() tâm I(3;-2), R=3.
tâm I(3;-2), R=3.
Gọi A(1;2), B(5;2) và E(3;2) là trung điểm của AB suy ra P=MA+MB
Lại có
![]()
![]() P lớn nhất
P lớn nhất  ME lớn nhất.
ME lớn nhất.
Mà ![]()
Vậy ![]()
z 1 = 3 ; z 2 = 4 ; z 1 - z 2 = 5 ⇒ OA=3; OB=4,AB=5 ⇒ ∆ O A B vuông tại O
⇒ S ∆ O A B = 1 2 . O A . O B = 1 2 . 3 . 4 = 6
Chọn đáp án C.