Cho tứ diện ABCD, gọi G 1 , G 2 lần lượt là trọng tâm các tam giác BCD và ACD . Mệnh đề nào sau đây SAI?
A. G 1 G 2 ∥ A B D
B. G 1 G 2 ∥ A B C
C. G 1 G 2 = 2 3 A B
D. Ba đường thẳng B G 1 , A G 2 và CD đồng quy.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
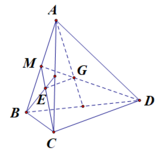
Gọi M là trung điểm của AB .
Có G là trọng tâm tam giác ABC nên G M D M = 1 3
Và E là trọng tâm tam giác ABC nên E M C M = 1 3
Áp dụng định lý Ta – lét có : G E // D C .

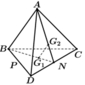
Gọi N là trung điểm của CD
● Khi đó A, G 2 , N thẳng hàng và B, G 1 , N thẳng hàng.
Do đó, B G 1 , A G 2 và CD đồng quy
![]() Áp dụng định lí Talet đảo, suy ra
Áp dụng định lí Talet đảo, suy ra
![]()
![]()
Do đó D sai. Chọn D.