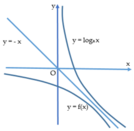
Biết đồ thị hàm số y = log a x và y = f ( x ) đối xứng nhau qua đường thẳng y = - x (như hình vẽ). Giá trị f - log a 3 là
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

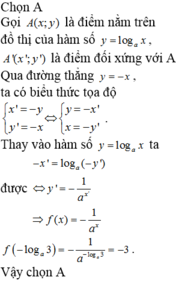

Chọn A
Gọi A(x;y) là điểm nằm trên đồ thị của hàm số y = log a x , A(x',y') là điểm đối xứng với A qua đường thẳng y = -x,
ta có biểu thức tọa độ 
Thay vào hàm số
y
=
log
a
x
ta được 


Vậy chọn A

Chọn A
Cách giải:
Đặt X= -x, Y=y => Ta có hệ trục tọa độ OXY như hình vẽ
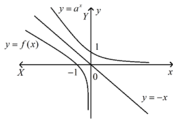
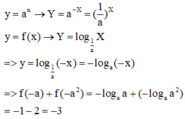

Có thể nghịch suy để chọn hàm làm trắc nghiệm
Do \(x_2=\dfrac{x_3-x_1}{2}=1\) nên hàm có dạng: \(y=a\left(x-1\right)^4-b\left(x-1\right)^2+c\) với a;b;c dương
\(y'=0\Rightarrow\left[{}\begin{matrix}x-1=0\\\left(x-1\right)^2=\dfrac{b}{2a}\end{matrix}\right.\) \(\Rightarrow x_1;x_3\) thỏa mãn \(\left(x-1\right)^2=\dfrac{b}{2a}\) và \(f\left(x_2\right)=c\)
\(f\left(x_1\right)+f\left(x_3\right)+\dfrac{2}{3}f\left(x_2\right)=0\Leftrightarrow2f\left(x_1\right)+\dfrac{2}{3}f\left(x_2\right)=0\)
\(\Leftrightarrow a.\left(\dfrac{b}{2a}\right)^2-b\left(\dfrac{b}{2a}\right)+c+\dfrac{c}{3}=0\Rightarrow-\dfrac{b^2}{4a}+\dfrac{4c}{3}=0\)
Tới đây chọn \(a=3;c=1;b=4\) được hàm \(f\left(x\right)=3\left(x-1\right)^4-4\left(x-1\right)^2+1\)
Dễ dàng tính ra \(x_3=1+\sqrt{\dfrac{2}{3}}\) ; \(x_0=1+\sqrt{\dfrac{1}{3}}\) (với \(x_0\) là giao bên phải của đồ thị và trục hoành); \(f\left(x_1\right)=f\left(x_3\right)=-\dfrac{1}{3}\)
\(S_1+S_2=\int\limits^{x_0}_1f\left(x\right)dx-\int\limits^{x_3}_{x_0}f\left(x\right)dx\approx0,41\)
\(\dfrac{S_1+S_2}{S_3+S_4}=\dfrac{0,41}{\left(1+\dfrac{1}{3}\right)\left(x_3-1\right)-0,41}\approx0,6\)

Với hàm số y=f(-2x+1) có
![]()
![]()
![]()
Với hàm số y=g(ax+b) có
y'=a.g'(ax+b)>0 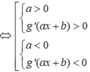
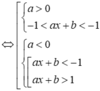
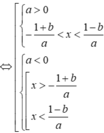
Vì hai hàm số đã cho có cùng khoảng đồng biến nên rơi vào trường hợp
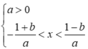 và
và 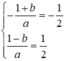
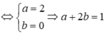
*Chú ý đồ thị đi lên hàm số đồng biến; đồ thị đi xuống hàm số nghịch biến.
Chọn đáp án C.

Trên đoạn [0;9] có f '(x) ⇔ x=0;x=;x=6
Bảng biến thiên :
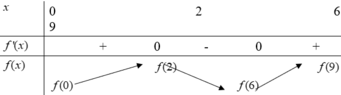
Suy ra ![]()
Quan sát các diện tích hình phẳng có :
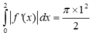
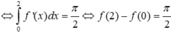
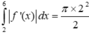
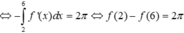
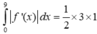
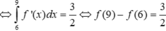
Suy ra
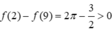
![]()
Chọn đáp án D.