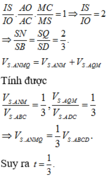Cho hình chóp S.ABCD. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, SB,SC. Mặt phẳng (MNP) cắt cạnh SD tại điểm Q. Đặt t = V S . M N P Q V S . A B C D . Tìm t.
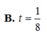
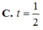
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()

Xét ΔSAB có \(\dfrac{SM}{SA}=\dfrac{SN}{SB}=\dfrac{1}{2}\)
nên MN//AB
Xét ΔSBC có \(\dfrac{SN}{SB}=\dfrac{SP}{SC}=\dfrac{1}{2}\)
nên NP//CD
Xét ΔSDC có \(\dfrac{SP}{SC}=\dfrac{SQ}{SD}=\dfrac{1}{2}\)
nên PQ//CD
MN//AB
AB\(\subset\left(ABCD\right)\)
MN không nằm trong mp(ABCD)
Do đó: MN//(ABCD)
NP//BC
BC\(\subset\)(ABCD)
NP không nằm trong mp(ABCD)
Do đó: NP//(ABCD)
PQ//CD
CD\(\subset\)(ABCD)
PQ không nằm trong mp(ABCD)
Do đó: PQ//(ABCD)
MN//(ABCD)
NP//(ABCD)
MN,NP cùng nằm trong mp(MNP)
Do đó: (MNP)//(ABCD)
NP//(ABCD)
PQ//(ABCD)
NP,PQ cùng nằm trong mp(NPQ)
Do đó: (NPQ)//(ABCD)
(MNP)//(ABCD)
(NPQ)//(ABCD)
Do đó: M,N,P,Q đồng phẳng

Chọn A
Gọi O là gia điểm của hai đường chéo của hình bình hành ABCD. Gọi I là giao điểm của SO và AM. Khi đó