Cách thực hiện nào sau đây vẫn cho phép tiếp tục ngắm chừng ở vô cực?
A. Dời vật
B. Dời thấu kính
C. Dời mắt
D. Ghép sát đồng trục một thấu kính
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
13 tháng 5 2019
Từ công thức: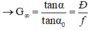 
→ G∞ không phụ thuộc vào khoảng cách kính – Mắt ⇒ Để tiếp tục ngắm chừng ở vô cực ta có thể dời mắt.
Đáp án: C
VT
2 tháng 6 2019
+ Vì cả hai vị trí đều cho ảnh lớn hơn vật nên thấu kính là hội tụ.
+ Trường hợp (1) cho ảnh thật bằng 3 lần vật nên ta có:
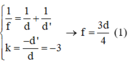
+ Khi dời vật vào gần thấu kính thì nó cho ảnh ảo bằng 3 lần vật nên ta có:
VT
29 tháng 9 2017
Chọn đáp án B
+ Thấu kính phân ki vật thật luôn cho ảnh ảo nhỏ hcm vật. Thấu kính hội tụ vật thật đặt trong tiêu cự cho ảnh ảo lớn hơn vật, vật thật đặt đặt cách thấu kính từ f đến 2f cho ảnh thật lớn hơn vật, và vật thật đặt cách thấu kính lớn hơn 2f cho ảnh thật nhỏ hơn vật.
+ Hai ảnh có cùng độ lớn thì một ảnh là ảnh thật (ảnh đầu) và một ảnh là ảnh ảo (ảnh sau).
VT
16 tháng 1 2017
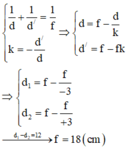
Đáp án C
Công thức tính bội giác của kính lúp ngắm chừng ở vô cực : 
G ∞ không phụ thuộc vào khoảng cách từ kính đến mắt
Để tiếp tục ngắm chừng ở vô cực thì ta có thể dời mắt
VT
25 tháng 9 2017
Chọn D
Sơ đồ tạo ảnh (mắt sát O2):
A B ⎵ d 1 → O 1 A 1 B 1 ⎵ d 1 / d 2 ⎵ l → O 2 A 2 B 2 ⎵ d 2 / d M ∈ O C C ; O C V ⎵ 0 → M a t V
d M = O C V = ∞ ⇒ d 2 / = − d M = − ∞ ⇒ d 2 = f 2 = 4 c m
⇒ d 1 / = l − d 2 = 34 − 4 = 30 = f ⇒ d 1 = ∞
+ Từ
α α 0 ≈ tan α tan α 0 = A 2 B 2 A 2 O 2 A B A O 2 = k A B d M A B d 1 + l = d 1 / d 2 / d 1 d 2 d 1 + l d M = 30 − ∞ ∞ .4 ∞ + l ∞ = 7 , 5
VT
19 tháng 10 2018
Ảnh của vật tạo bởi thấu kính trong cả hai trường hợp đều lớn hơn bằng ba lần vật.
Một trường hợp sẽ là ảnh thật và trường hợp còn lại sẽ là ảnh ảo
Một thấu kính mà có thể tạo được ảnh ảo lớn gấp ba lần vật thì đó là thấu kính hội tụ.
Đáp án: A
Đáp án C