cho tam giác ABC có A = 30 độ, trên tia đối của tia AC lấy D sao cho CD=CA trên tia đối của CB Lấy E sao cho CE=CB tính số đo góc CDE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 9 2016
Hình bạn tự vẽ nhé!
Xét tam giác ABC và tam giác DEC có:
CB = CE (gt)
góc BCA = góc ECD ( đối đỉnh)
CA = CD (gt)
=> Tam giác ABC = Tam giác DEC (c.g.c)
=> góc CAB = góc CDE (2 góc tương ứng)
mà góc CAB = 90 độ
=> góc CDE = 90 độ.
Vậy góc CDE = 90 độ
NM
22 tháng 8 2016
xét tg abc và tg edc có
bc = ec ( gt )
góc bca = góc dce ( 2 góc đối đỉnh )
ac = dc
abc = edc
suy ra góc bac = góc cde = 90 độ
22 tháng 8 2016
nhớ tick cho mk nha, mk sẽ trả lười câu hỏi này giúp bn:hjhj
Xét tam gjac ABC và tam gjac ECD:
AC=CD (giả thiết)
BC=CE (giả thiết)
góc ACB=góc ECD
Do đó tam gjac ABC=tam gjac ECD (c.g.c)
\(\Rightarrow\)góc A= góc D = 90o (vì 2 tam gjac = nhau có các góc tương ứng = nhau ).
Vậy góc CDE= 90o (góc vuông)
hjhj đây lak cách gjai của mk đó.
CM
5 tháng 5 2017
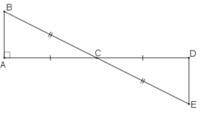
Xét ΔABC và ΔDEC, ta có:
AC = DC (gt)
∠(ACB) =∠(ECD) (đối đỉnh)
BC=EC (gt)
Suy ra: ΔABC= ΔDEC (c.g.c)
⇒∠A =∠D ̂(hai góc tương ứng).Mà ∠A =90o nên ∠D =90o
31 tháng 12 2021
Xét tứ giác ABDE có
C là trung điểm của AD
C là trung điểm của BE
Do đó: ABDE là hình bình hành
Suy ra: AB//DE
hay DE⊥AC
=>\(\widehat{CDE}=90^0\)