Cho hình chóp O.ABC có OA=OB=OC=a, A O B ^ = 60 o , B O C ^ = 90 o , C O A ^ = 120 o . Gọi S là trung điểm của OB. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là
A. a 4
B. a 7 4
C. a 7 2
D. a 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

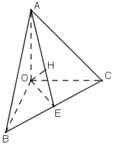

- Tam giác OBC vuông ở O và có đường cao OE nên:
1 O E 2 = 1 O B 2 + 1 O C 2 5
- Tam giác AOE vuông ở O và có đường cao OH nên:
1 O H = 1 O A 2 + 1 O E 2
Từ (5) và (6) suy ra
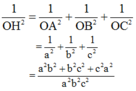
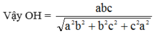

a) Ta có: \(\left. \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right)\)
Mà \(BC \in \left( {OBC} \right) \Rightarrow OA \bot BC\)
b) Ta có \(\left. \begin{array}{l}OA \bot OB\\OB \bot OC\end{array} \right\} \Rightarrow OB \bot \left( {OAC} \right)\)
Mà \(CA \in \left( {OAC} \right) \Rightarrow CA \bot OB\)
c) Ta có \(\left. \begin{array}{l}OC \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OC \bot \left( {OAB} \right)\)
Mà \(AB \in \left( {OAB} \right) \Rightarrow AB \bot OC\)
Gọi M là trung điểm của SB, trong (SBH) kẻ đường thẳng vuông góc với SB cắt OH tại I.