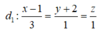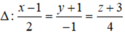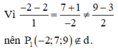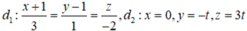Trong không gian Oxyz. Đường thẳng đi qua M(1;2;-3) nhận vec tơ làm vec tơ chỉ phương có phương trình là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A
Phương pháp:
Đường thẳng đi qua M x 0 ; y 0 ; z 0 và có VTCP là u → =(a;b;c) có phương trình chính tắc:
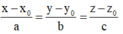
Cách giải: Đường thẳng d đi qua M(2;0;-1) và có VTCP là u → =(2;-3;1) có phương trình chính tắc:
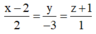

Đáp án A
Gọi A = d ∩ d 2 . Ta có A ∈ d 2 => A(-1; a; a+ 1).
Theo giả thiết:
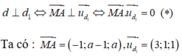
Thay vào (*) ta được:
-1.3 + (a - 1).1 + a.1 = 0 <=> 2a - 4 = 0 <=> a = 2 <=> u d → = MA → = (-1; 1; 2)
Vậy phương trình chính tắc của đường thẳng d là: 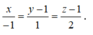
Vậy đáp án đúng là A.

Đáp án D
∆ có véc tơ chỉ phương là u → = 2 ; 1 - 1 . Gọi N là giao điểm của d và ∆ ⇒ N 2 t + 1 ; t - 1 ; - t
Theo đề bài ta sẽ có: u → . M N → = 0 ⇔ t = 2 3 ⇒ M N → = 1 3 ; - 4 3 ; - 2 3 ⇒ d : x - 2 1 = y - 1 - 4 = z - 2

Đáp án B
Đường thẳng ∆ có vecto chỉ phương u → (2; -3; 2)
Đường thẳng d đi qua M(4;3;1) và song song với đường thẳng ∆ nên có vecto chỉ phương là u → (2; -3; 2). Phương trình chính tắc của đường thẳng d là:
![]()

Chọn D
Phương pháp:
Phương trình tham số của đường thẳng đi qua điểm


Chọn D.
Phương pháp:
Phương trình tham số của đường thẳng đi qua điểm