Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
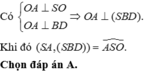
a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
b: (SA;(SBD))=(SA;SO)=gócASO
Xét ΔACB có BA=BC và góc ABC=60 độ
nên ΔBAC đều
=>AO=a/2
\(SA=\sqrt{SO^2+OA^2}=\sqrt{a^2+\dfrac{1}{4}a^2}=\dfrac{\sqrt{5}}{2}\cdot a\)
sin ASO=OA/SA=a/2:a*căn 5/2
\(=\dfrac{\sqrt{5}}{5}\)
=>góc ASO=27 độ
Đáp án A.
Gọi H là hình chiếu của C trên SO và góc S O C ^ tù nên H nằm ngoài đoạn SO => CH ⊥ (SBD)
=> Góc tạo bởi SC và (SBD) là C S O ^
Lại có 
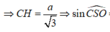
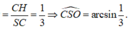
Có : AC vuông góc với BD (hình vuông ABCD)
SA vuông góc với BD ( do SA vuông góc với mp ABCD)
=> BD vuông góc với mp SAC...
a) Gọi O là tâm của hình thoi, ta có AC ⊥ BD tại O
Vì SA = SC nên SO ⊥ AC.
Do đó AC vuông góc với mặt phẳng (SBD)
Ta suy ra mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD).
b) Ba tam giác SAC, BAC, DAC bằng nhau ( c.c.c) nên ta suy ra OS = OB = OD. Vậy tam giác SBD vuông tại S.
