Cho lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy a=3. Biết tam giác A'BA có diện tích bằng 6. Thể tích tứ diện ABB'C' bằng:
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

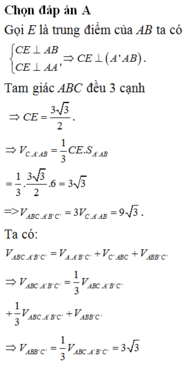
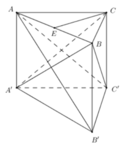

Gọi E là trung điểm BC → AE vuông góc (vg) với BC
mà (ABC) vg (BB'C'C)
→ AE vg (BB'C'C)
\(V_{A.BB'C'C}=\frac{1}{3}\cdot AE\cdot S_{BB'C'C}=\frac{1}{3}\cdot\frac{a\sqrt{3}}{2}\cdot BB'\cdot BC=\frac{a^3\sqrt{3}}{3}\)
Vì SBB'C = 1/2 * SBB'C'C
nên VABB'C' = 1/2 * VA.BB'C'C = (a3căn3)/6

Đáp án A
Gọi H là trung điểm của BC, giao điểm của (P) và A A ' là P.
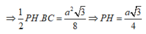

∆ A H P vuông tại P có A P = A H 2 - P H 2 = 3 a 4
∆ A A ' O ~ ∆ A H P ⇒ A ' O A O = H P A P
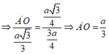
⇒ V A B C . A ' B ' C ' = O A ' . S A B C = a 3 3 12

Đáp án là C
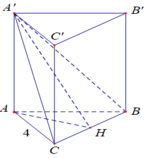
Δ A B C đều cạnh a = 4 nên S Δ A B C = 4 3 .
Gọi H là trung điểm B C của . Ta có: A H = 2 3 và B C ⊥ A ' A H ⇒ B C ⊥ A ' H
Và S Δ A ' B C = 1 2 B C . A ' H ⇒ A ' H = 4
Δ A ' A H vuông tại A nên A A ' = A ' H 2 − A H 2 = 2 .
V A B C . A ' B ' C ' = A A ' . S Δ A B C = 2.4 3 = 8 3 .