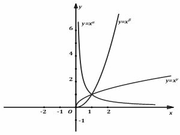
Cho các hàm số lũy thừa y = x ∝ , y = x β , y = x γ có đồ thị như hình vẽ. Mệnh đề đúng là:
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()


Đáp án D
Hàm số x α nghịch biến do đó 0 < α < 1 .
Các hàm số x β , x γ là các hàm số đồng biến do đó β , γ > 1 .
Cho x = 100 ⇒ 100 β > 100 γ ⇒ β > γ .

Đáp án D
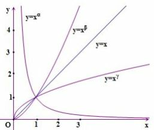
Với x > 1 mà lim x α = 0 ⇔ 0 < a < 1 và cũng suy ra β , γ > 1
Với x > 1 , với cùng 1 giá trị x 0 thì x β > x γ ⇒ β > γ .

Đáp án là C
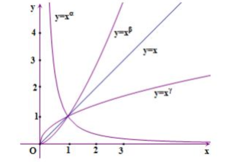
Từ đồ thị hàm số ta có
Hàm số y = x α nghịch biến trên (0; + ∞ ) nên a < 0.
Hàm số y = x β , y = x γ đồng biến trên (0; + ∞ ) nên .
Đồ thị hàm số y = x β nằm phía trên đồ thị hàm số y = x khi x >1 nên b >1.
Đồ thị hàm số y = x γ nằm phía dưới đồ thị hàm số y = x khi x >1 nên g <1.
Vậy a < 0 < g < 1 < b

Đáp án D
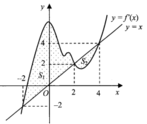
Gọi S1, S2 lần lượt là diện tích hình phẳng như hình vẽ.
Ta có: ![]()
![]()
Tương tự ![]() (2)
(2)
Từ đồ thị ta có: ![]()
Từ (1), (2), (3) suy ra ![]()

Chọn A
Nhìn vào đồ thị hàm số ![]() ta thấy
ta thấy ![]() để
để ![]()
Bảng biến thiên của hàm số ![]()
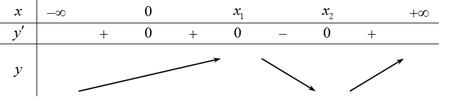
KL: Hàm số ![]() có 1 điểm cực đại và 1 điểm cực tiểu.
có 1 điểm cực đại và 1 điểm cực tiểu.