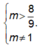Các giá trị của tham số m để đồ thị của hàm số y = x - 1 m x 2 - 3 m x + 2 có bốn đường tiệm cận phân biệt là
A. m > 0
B. m > 9 8
C. m > 8 9
D. m > 8 9 , m ≠ 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 8 2019
Đáp án là D.
Đồ thị hàm số có bốn đường tiệm cận khi phương trình m 2 x 2 + m − 1 = 0 có hai nghiệm phân biệt khác -1 ⇔ m 2 ≠ 0 − m 2 m − 1 > 0 ⇔ m ≠ 0 m < 1 .
CM
29 tháng 12 2017
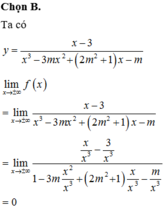
Nên y = 0 là tiệm ngang của đồ thị hàm số.
Vậy để đồ thị hàm số có 4 đường tiệm cận thì đồ thị hàm số phải có 3 đường tiệm cận đứng.
Hay phương trình
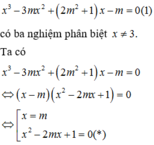
Để phương trình (1) có ba nghiệm phân biệt khác 3 thì m khác 3 và phương trình (*) có hai nghiệm phân biệt khác m và khác 3.
Do đó
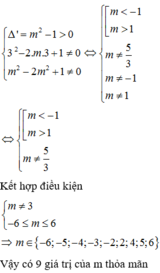
Chọn D.
Đồ thị hàm số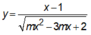
có bốn đường tiệm cận phân biệt
⇔
Đồ thị hàm só có 2 đường tiệm cận đứng và 2 đường tiệm cận ngang phân biệt.
Đồ thị hàm số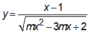
có 2 đường tiệm cận ngang phân biệt
Với m > 0, khi đó ta có:
Đồ thị hàm số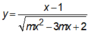
có 2 đường tiệm cận đứng phân biệt
Từ (1) và (2) ta được