Hình bên là đồ thị của ba hàm số y = a x , y = b x , y = c x 0 < a , b , c ≠ 1 được vẽ trên cùng một hệ trục trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?
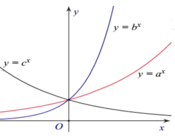
A. b>a>c
B. a>b>c
C. a>c>b
D. c>b>a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhận xét:
+) Đồ thị hàm số y = x a nghịch biến trên khoảng ( 0 ; + ∞ ) ⇒ a < 0
+) Xét đồ thị hàm số y = log b x v à y = log c x , x > 0
Cho y=1 ta có: log b x 1 = log c x 2 ⇔ x 1 = b , x 2 = c
Mà x 1 < x 2 ⇒ b < c ⇒ a < 0 < b < c . Vậy a<b<c
Chọn đáp án D.

Hàm số \(y=log_cx\) nghịch biến
\(\Rightarrow0< c< 1\) và các hàm \(y=log_ax,y=log_bx\) đồng biến nên \(a,b>1\)
Ta chọn \(x=100\Rightarrow log_a>log_b100\Rightarrow a< b\Rightarrow b>a>c\)
\(\Rightarrow B\)

\(-\) Do \(c^x\) nghịch biến\(,a^x,b^x\) đồng biến\(\Rightarrow c< 1,a>1,b>1\Rightarrow c\) nhỏ nhất \(\Rightarrow\)Loại \(C,D\)
\(-\) Dựa vào đồ thị ta thấy\(,b^x\) có đồ thị đi lên cao hơn so với \(a^x\Rightarrow b>a\Rightarrow\) Chọn \(A\)
Đáp án A
Do y = a x và y = b x là hai hàm đồng biến nên a;b>1
Do y = c x nghịch biến nên c<1 Vậy c bé nhất.
Mặt khác: Lấy x = m , khi đó tồn tại y 1 , y 2 > 0 a m = y 1 b m = y 2
Dễ thấy y 1 < y 2 ⇒ a m < b m ⇒ a < b
Vậy b>a>c.