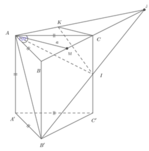
Cho lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác cân, AB = AC = a, BAC = 120 ° BB' = a, I là trung điểm CC'. Gọi α là góc giữa hai mặt phẳng (ABC) và (AB'I). Tính cos α
A. c o s α = 3 10
B. c o s α = 3 10
C. c o s α = 3 10
D. c o s α = 3 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Phương pháp:
Cách giải: Gọi J là giao điểm của B’I và BC. Suy ra AJ là giao tuyến của (AB’I) và (ABC).
Gọi K là hình chiếu của C lên AJ. Suy ra AJ vuông góc với KI.

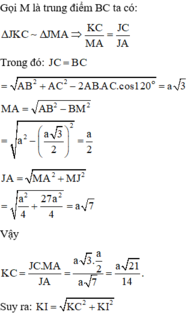
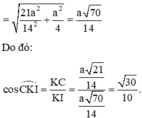

Đáp án B
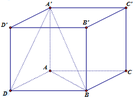
Gọi a là độ dài cạnh hình lập phương. Thể tích khối lập phương: V 1 = a 3
Thể tích khối tứ diện: A B D A ' : V 2 = 1 3 . A A ' . S A B D = 1 3 . a . a 2 2 = a 3 6
Vậy V 1 = 6 V 2

Đáp án C
Phương pháp: Cách xác định góc giữa hai mặt phẳng:
- Tìm giao tuyến của hai mặt phẳng.
- Góc giữa hai mặt phẳng là góc giữa hai đường thẳng nằm trong hai mặt phẳng và vuông góc với giao tuyến.
Cách giải: Gọi E là giao điểm của B’I và BC.
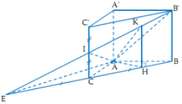
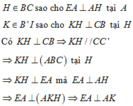
Hai mặt phẳng (AIB') và (ACB) có giao tuyến là EA
mà A K ⊂ A I B ' ; A H ⊂ A C B ; E A ⊥ A K ; E A ⊥ A H ⇒ hợp bởi hai mặt phẳng (AIB') và (ACB) là KAH
Ta có: B C = 2 a cos 30 ° = a 3
A E 2 = E C 2 + A C 2 − 2 A C . E C . cos A C E = 3 a 2 + a 2 − 2 a . a 3 . cos 150 ° = 7 a 2 ⇒ A E = a 7
Ta có:
cos A E C = A E 2 + E C 2 − A C 2 2 A C . E C = 7 a 2 + 3 a 2 − a 2 2 a 7 . a 3 = 9 2 21
⇒ tan A E C = 1 cos 2 A E C − 1 = 3 9 . ⇒ A H = A E . tan A E C = a 21 9
Ta có: E H E B = H K B B '
⇒ H K = E H . B B ' E B = A E . B B ' 2 B C . cos A E C = a 7 . a .2 21 2 a 3 .9 = 7 a 9
cos K A H = A H A K = A H A H 2 + H K 2 = a 21 9 21 a 2 81 + 49 a 2 81 = 30 10