Gọi (P) là đường parabol đi qua ba điểm cực trị của đồ thị hàm số y = m x 4 - m 2 + 1 x 2 + m 2 - m + 1 và A, B là giao điểm của (P) với trục hoành. Khi AB = 2, mệnh đề nào dưới đây đúng?
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1

Đáp án C
y = 1 4 x 4 − m x 2 + m 2 y ' = x 3 − 2 m x = x x 2 − 2 m
Để hàm số có 2 cực trị ⇔ x 2 − 2 m = 0 có hai nghiệm phân biệt khác 0
⇔ 2 m > 0 ⇔ m > 0
D 0 ; m 2 , B − 2 m ; 0 ; C 2 m ; 0
Gọi P : y = a x 2 + b x + c , ( a ≠ 0 ) là parabol đi qua 3 điểm cực trị D, B và C.
Suy ra c = m 2 2 m a − 2 m b + m 2 = 0 2 m a + 2 m b + m 2 = 0 ⇔ c = m 2 a = − m 2 b = 0
Do đó ( P ) : y = − m 2 x 2 + m 2
Vì A ( 2 ; 24 ) ∈ ( P ) nên
24 = − m 2 .4 + m 2 ⇔ m 2 − 2 m − 24 = 0 ⇔ m = − 4 ( L ) m = 6

Chọn đáp án D
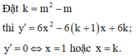
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi k ≠ 1
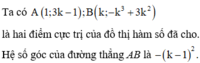
Đường thẳng AB vuông góc với đường thẳng y = x + 2 khi và chỉ khi


a, - Xét phương trình hoành độ giao điểm :\(x^2=\left(m-2\right)x-m+3\)
\(\Leftrightarrow x^2-\left(m-2\right)x+m-3=0\left(I\right)\)
Có \(\Delta=b^2-4ac=\left(m-2\right)^2-4\left(m-3\right)\)
\(=m^2-4m+4-4m+12=m^2-8m+16=\left(m-4\right)^2\)
- Để P cắt d tại 2 điểm phân biệt <=> PT ( I ) có 2 nghiệm phân biệt .
<=> \(\Delta>0\)
\(\Leftrightarrow\left(m-4\right)^2>0\)
\(\Leftrightarrow m\ne4\)
Vậy ...
b, Hình như đề thiếu giá trị của cạnh huỳnh hay sao á :vvvv
a) Phương trình hoành độ giao điểm là:
\(x^2=\left(m-2\right)x-m+3\)
\(\Leftrightarrow x^2-\left(m-2\right)x+m-3=0\)
\(\Delta=\left(m-2\right)^2-4\cdot\left(m-3\right)=m^2-4m+4-4m+12=m^2-8m+16\)
Để (d) cắt (P) tại hai điểm phân biệt thì \(\Delta>0\)
\(\Leftrightarrow m^2-8m+16>0\)
\(\Leftrightarrow\left(m-4\right)^2>0\)
mà \(\left(m-4\right)^2\ge0\forall m\)
nên \(m-4\ne0\)
hay \(m\ne4\)
Vậy: khi \(m\ne4\) thì (d) cắt (P) tại hai điểm phân biệt

TXĐ: D = R
\(y'=3x^2-6x=0\) \(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=1\\x=2\Rightarrow y=-3\end{matrix}\right.\)
Suy ra 2 điểm cực trị của đồ thị là: A(0; 1) và B(2; -3)
Ptđt đi qua 2 điểm cực trị:
\(\dfrac{x}{2}=\dfrac{y-1}{-4}\) \(\Rightarrow-2x=y-1\) \(\Leftrightarrow y=-2x+1\left(d'\right)\)
Vì \(d\perp d'\) \(\Rightarrow\left(2m-1\right)\cdot\left(-2\right)=-1\) \(\Leftrightarrow m=\dfrac{3}{4}\)
Chọn B

(P) đi qua điểm A (−2; 4) nên 4 = a. ( − 2 ) 2 = 4a a = 1
Vậy phương trình parabol (P) là y = x 2 .
Để (P) tiếp xúc với (d) thì phương trình hoành độ giao điểm
x 2 = 2 (m – 1)x – (m – 1)có nghiệm kép
↔ ∆ ’ = [ − ( m – 1 ) ] 2 − m + 1 = 0 ↔ m 2 – 2m + 1 − m + 1 = 0 ↔ m 2 – 3m + 2 = 0 ↔ m=1 hoặc m=2
Nếu m = 1 thì hoành độ giao điểm là x = 0. Vậy tiếp điểm là (0; 0)
Nếu m = 2 thì hoành độ giao điểm là x = 1. Vậy tiếp điểm là (1; 1)
Đáp án: C
Đáp án D.