Hình chóp tứ giác đều có cạnh đáy bằng a, chiều cao h = a 2 . Góc giữa cạnh bên với mặt đáy là:
A. 60 o
B. 15 o
C. 45 o
D. 30 o
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
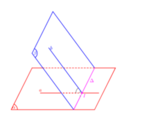

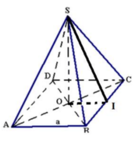
Gọi O là tâm của hình vuông ABCD. I là trung điểm của BC. Ta có:
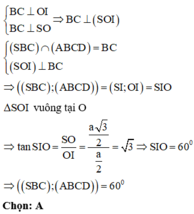

a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)

Chân đường cao hình chóp đều S.ABCD trùng với tâm O của đáy ABCD. AO là hình chiếu của SA lên (ABCD)
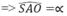
Đáp án C

Gọi O là tâm đáy, M là trung điểm AB
Ta có: \(\left\{{}\begin{matrix}SO\perp\left(ABC\right)\\OM\perp AB\end{matrix}\right.\) \(\Rightarrow\widehat{SMO}\) hay là góc giữa mặt bên và mặt đáy
\(\Rightarrow\widehat{SMO}=60^0\) \(\Rightarrow SO=OM.tan60^0=\dfrac{1}{3}CM.tan60^0=\dfrac{1}{3}AB.\dfrac{\sqrt{3}}{2}.tan60^0=\dfrac{a}{2}\)
\(CO=\dfrac{2}{3}CM=\dfrac{2}{3}.AB\dfrac{\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
\(SC=\sqrt{SO^2+OC^2}=\dfrac{a\sqrt{21}}{6}\)
Chọn C.
Gọi SO là đường cao của hình chóp tứ giác đều S.ABCD. Do đó góc giữa cạnh bên và mặt đáy là góc S B O ^
Ta có:
S O = h = a 2 ; O B = B D 2 = a 2
Tam giác vuông SBO tại O có SO=OB= a 2 nên cân tại O.
Suy ra S B O ^ = 45 o